# 剑指Offer
# 面试需要的基础知识
# 数据结构
| 结构 | 特点 | 用途 |
|---|---|---|
| 数组 | 最基本的数据结构 需要预先分配,空间利用率不好,有空闲区域 因为空间连续,O(1)时间读/写任何元素,时间效率很高 | 连续内存分别存储数字和字符串 实现哈希表 |
| 字符串 | 最基本的数据结构 | 连续内存分别存储数字和字符串 |
| 链表 | 高频,大量指针 空间利用率高 空间不连续,查找第i个节点,只能从头开始遍历 时间效率为O(n) | |
| 树 | 存在大量指针 | 索引 |
| 栈 | 先进后出 不考虑排序的数据结构 O(n)的时间找到最大或者最小元素,O(1)需要特殊处理 | 递归紧密相关 |
| 队列 | 先进先出 | 广度优先遍历算法 从上到下打印二叉树 |
# 树
面试提到的树,大多是二叉树,是一种特殊的树,每个节点做多只能有两个子节点。
最重要的莫过于遍历,按照某一种顺序遍历树中所有节点
遍历方式
- 前序遍历:先访问根节点,在访问左子节点,后访问右子节点
- 中序遍历:中序遍历,线访问左子节点,在访问根子节点,最后访问右子节点
- 后叙遍历:后序遍历,线访问左子节点,在访问右子节点,最后访问根节点
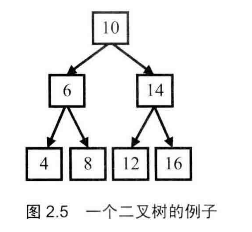
| 遍历方式 | 结果 |
|---|---|
| 前序遍历 | 10->6->4->8->14->12->16 |
| 中序遍历 | 4->6->8->10->12->14->16 |
| 后i序遍历 | 4->8->6->12->16->14=>10 |
# 二叉树特例:二叉搜索树
左子节点总是小于或者等于根节点,右子节点总是大于或者等于根节点
平均在O(logn)的时间内根据树枝在二叉梭梭树中找到一个接待你。
# 二叉树特例:堆
分为最大堆和最小堆,在最大堆中根节点的值最大,在最小堆中根节点的值最小
快速找到最大值或者最小值的问题都可以用堆来解决。
# 二叉树特例:红黑树
节点定义为红、黑两种颜色,并通过规则确保从 根节点到叶节点的最长路径长度 不超过最短路径的两倍
# 面试题7:重建二叉树
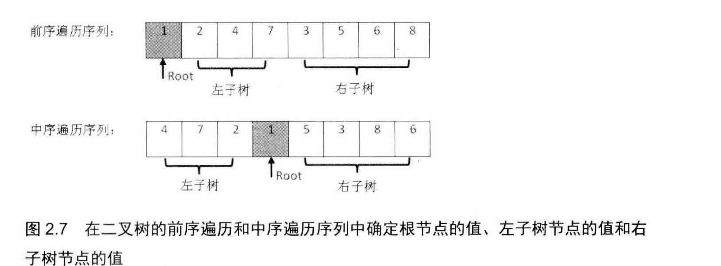
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建该二叉树,假设输入的前序遍历和中序遍历都不包含重复的数字,例如,输入前序遍历 {1,2,4,7,3,5,6,8} 和中序遍历 {4,7,2,1,5,3,8,6}

package com.lovedata.interview.N07_ConstructBinaryTree;
import utils.TreeNode;
import utils.TreeOperation;
import java.util.Arrays;
/**
* @author pengshuangbao
* @date 2021/2/8 11:44 AM
* * 输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
* * 例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
* <p>
* 1. 分析
* 根据中序遍历和前序遍历可以确定二叉树,具体过程为:
* <p>
* 根据前序序列第一个结点确定根结点
* 根据根结点在中序序列中的位置分割出左右两个子序列
* 对左子树和右子树分别递归使用同样的方法继续分解
* 例如:
* 前序序列{1,2,4,7,3,5,6,8} = pre
* 中序序列{4,7,2,1,5,3,8,6} = in
* <p>
* 根据当前前序序列的第一个结点确定根结点,为 1
* 找到 1 在中序遍历序列中的位置,为 in[3]
* 切割左右子树,则 in[3] 前面的为左子树, in[3] 后面的为右子树
* 则切割后的左子树前序序列为:{2,4,7},切割后的左子树中序序列为:{4,7,2};切割后的右子树前序序列为:{3,5,6,8},切割后的右子树中序序列为:{5,3,8,6}
* 对子树分别使用同样的方法分解
*/
public class ConstructBinaryTree {
public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
TreeNode root = reConstructBinaryTree(pre, 0, pre.length - 1, in, 0, in.length - 1);
return root;
}
private TreeNode reConstructBinaryTree(int[] pre, int preStart, int preEnd, int[] in, int inStart, int inEnd) {
// 确认边界
if (preStart > preEnd || inStart > inEnd) {
return null;
}
//前绪遍历的第一个节点就是根节点
int rootVal = pre[preStart];
TreeNode root = new TreeNode(rootVal);
//然后切割,在中序遍历中,根节点前面的,就是左边的节点,根节点右边的,就是右边的节点
for (int i = inStart; i <= inEnd; i++) {
if (in[i] == rootVal) {
root.left = reConstructBinaryTree(pre, preStart + 1, preStart + i - inStart, in, inStart, i - 1);
root.right = reConstructBinaryTree(pre, preStart + i - inStart + 1, preEnd, in, i + 1, inEnd);
}
}
return root;
}
private TreeNode reConstructBinaryTreeCopy(int[] pre, int[] in) {
// * 前序序列{1,2,4,7,3,5,6,8} = pre
// * 中序序列{4,7,2,1,5,3,8,6} = in
if (pre == null || in == null || pre.length == 0 || in.length == 0) {
return null;
}
int rootVal = pre[0];
if (rootVal == 4) {
System.out.println();
}
TreeNode root = new TreeNode(rootVal);
for (int i = 0; i < in.length; i++) {
if (in[i] == rootVal) {
//左子树,注意 copyOfRange 函数,左闭右开
root.left = reConstructBinaryTreeCopy(Arrays.copyOfRange(pre, 1, i + 1), Arrays.copyOfRange(in, 0, i));
//右子树,注意 copyOfRange 函数,左闭右开
root.right = reConstructBinaryTreeCopy(Arrays.copyOfRange(pre, i + 1, pre.length), Arrays.copyOfRange(in, i + 1, in.length));
}
}
return root;
}
public static void main(String[] args) {
ConstructBinaryTree constructBinaryTree = new ConstructBinaryTree();
TreeNode treeNode = constructBinaryTree.reConstructBinaryTree(new int[]{1, 2, 4, 7, 3, 5, 6, 8}, new int[]{4, 7, 2, 1, 5, 3, 8, 6});
TreeOperation.show(treeNode);
TreeNode treeNode1 = constructBinaryTree.reConstructBinaryTreeCopy(new int[]{1, 2, 4, 7, 3, 5, 6, 8}, new int[]{4, 7, 2, 1, 5, 3, 8, 6});
TreeOperation.show(treeNode1);
}
}
# 面试题8:二叉树的下一个节点
给定一颗二叉树和其中的一个节点,如何找出中序遍历序列的下一个节点?树中的节点除了有两个分别智商左、右子节点的指针,还有一个指向父节点的指针
中序遍历序列是{d,b,h,,e,i,a,f,c,g}
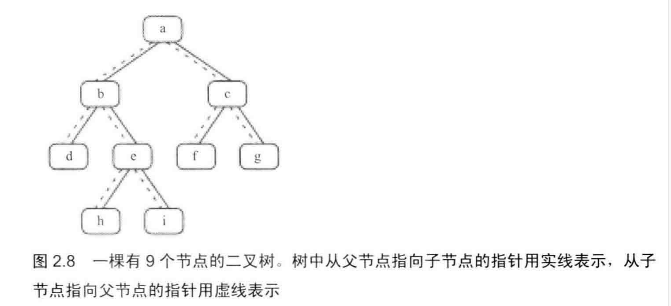
两种情形:
- 如果有右子树,那么它的下一个节点就是它的右子树中的最左节点。一直找左子树指针,找到最左的那个。
- 没有右子树,如果节点是它父节点的左子节点,那么它的下一个节点就是它的父节点
- 如果节点没有右边子树,并且还是父节点的右子节点,可以沿着父节点向上遍历,直到找到一个是它它父亲节点左子节点的节点,如果这个节点存在,那么这个节点的父节点就是我们要找的下一个节点
/**
* @author pengshuangbao
* @date 2021/2/8 2:45 PM
*/
public class NextNodeInBinaryTrees {
public TreeLinkNode getNext(TreeLinkNode node) {
if (node == null) {
return null;
}
//如果有右子树,那么它的下一个节点就是它的右子树中的最左节点。
// 一直找左子树指针,找到最左的那个。
if (node.right != null) {
TreeLinkNode next = node.right;
while (next.left != null) {
next = next.left;
}
return next;
}
// 如果当前子结点pNode右子树为空
// 返回上层的父结点,如果父结点的右子结点就是当前结点,继续返回到上层的父结点...直到父结点的左子结点等于当前结点
while (node.next != null && node.next.right == node) {
node = node.next;
}
// 如果父结点的左子结点等于当前结点,说明下一个要遍历的结点就是父结点了;或者父结点为空(说明当前结点是root),还是返回父结点(null)
// pNode.next == null 或者 pNode.next.left == pNode
return node.next;
}
}
# 栈和队列
操作系统线程使用栈来存储函数调用时哥哥函数的参数,返回地址和临时遍历那个。
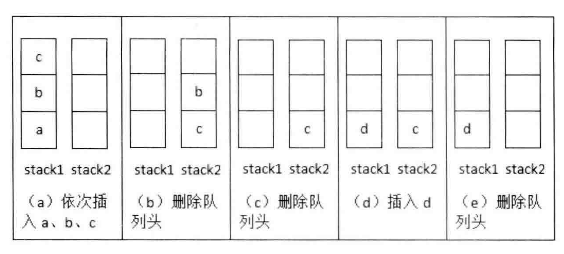
# 面试题9:用两个栈实现队列
用两个栈实现一个队列,队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead,分别完成在队列尾部插入节点和队列头部插入节点的功能。
使用两个 先进后出的栈 实现一个先进先出的队列
package com.lovedata.interview.N09_QueueWithTwoStacks;
import java.util.LinkedList;
/**
* @author pengshuangbao
* @date 2021/2/8 3:11 PM
*/
public class QueueWithTwoStacks {
private LinkedList<String> stack1 = new LinkedList<String>();
private LinkedList<String> stack2 = new LinkedList<String>();
public void appendTail(String element) {
stack1.push(element);
}
public String deleteHead() {
if (stack1.isEmpty() && stack2.isEmpty()) {
throw new RuntimeException("error");
}
if (stack2.size() <= 0) {
while (!stack1.isEmpty()) {
String pop = stack1.pop();
stack2.push(pop);
}
}
if (stack2.size() == 0) {
throw new RuntimeException("error");
}
return stack2.pop();
}
}
# 算法和数据操作
通过排序和查找是重点
重带你掌握二分查找、归并排序和快速排序
位运算可以堪称一类特殊的算法,它是把数字表示成二进制之后堆0 和 1 的操作,由于位运算的对象为二进制数字,所以并不是很直观。
总共有 与 、 或、 异或、 左移 、 右移 五种位运算
# 递归和循环
需要重复多次计算相同的问题,通常用递归或者循环两种。
递归是函数内部调用函数自身,循环是设置计算初始值和终止条件,在一个范围内重复运算
package utils;
/**
* @author pengshuangbao
* @date 2021/2/8 3:58 PM
*/
public class AddFromToN {
public int addFromToNRecursive(int n) {
return n <= 0 ? 0 : n + addFromToNRecursive(n - 1);
}
public static void main(String[] args) {
AddFromToN add = new AddFromToN();
System.out.println(add.addFromToNRecursive(2));
}
public int addFromToNTerative(int n) {
int result = 0;
for (int i = 1; i <= n; i++) {
result += i;
}
return result;
}
}
# 递归优缺点
递归更加简洁,如果没有特殊要求,尽量使用递归实现函数
缺点:
- 函数调用自身,函数调用是有时间和空间小号的:每次调用都需要在栈中分配空间以保存参数、返回地址和临时变量,栈的压入和弹出都是需要时间的,所以效率上不如循环。
- 很多计算是重复的,本质是大问题分解成一个个小问题,小问题存在相互重叠的部分,就存在重复的计算。
- 容易存在调用栈溢出。
# 面试题10: 斐波那契额数列
求斐波那契数列的第n项
写一个函数,输入n,求斐波那契额(Fibonacci)数列的第n项。定义如下
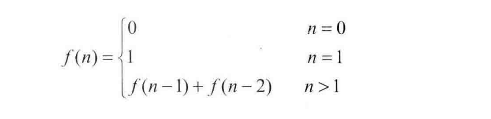
package com.lovedata.interview.N10_Fibonacci;
/**
* @author pengshuangbao
* @date 2021/2/8 4:23 PM
*/
public class Fibonacci {
/**
* 递归求斐波那契,性能较差
*
* @param n
* @return
*/
public int fibonacci(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci(n - 2);
}
/**
* 推荐的性能较好的解法
* 时间复杂度O(n)
*
* @param n
* @return
*/
public int fibonacci2(int n) {
if (n == 0) {
return 0;
}
if (n == 1) {
return 1;
}
int fiboN = 0;
int a = 1;
int b = 0;
for (int j = 2; j <= n; j++) {
fiboN = a + b;
b = a;
a = fiboN;
}
return fiboN;
}
public static void main(String[] args) {
long start = System.currentTimeMillis();
Fibonacci fib = new Fibonacci();
System.out.println(fib.fibonacci(3));
System.out.println(System.currentTimeMillis() - start);
long start1 = System.currentTimeMillis();
System.out.println(fib.fibonacci2(20));
System.out.println(System.currentTimeMillis() - start1);
}
}
# 查找和排序
# 查找
查找相对于简单,顺序查找、二分查找、哈希表查找、二叉排序树查找。
如果要求在排序的数组(或者部分排序的数组)查找一个数字或者统计某个数字出现的次数,可以尝试用二分查找算法。
# 哈希表优缺点
优点:主要优点可以利用它能够在O(1)的时间内查找某一个元素,是效率最高的查找方式
缺点: 需要额外的空格你就爱你来实现哈希表
# 排序
排序比查找复杂些,比较插入排序、冒泡排序、归并排序、快速排序等不同算法的优劣。一定要对各种排序算法特点烂熟于胸。
能从 额外空间小号、平均时间复杂度和最差时间复杂度等方面比较优缺点
编程题-快速排序 | 编程手册 (opens new window)
十大经典排序算法动画,看我就够了! - 云+社区 - 腾讯云 (opens new window)

# 面试题11: 旋转数组中的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
两种解法:
- 利用遍历一边,对比 i 于 i+1 的大小,如果 i> (i+1) 则,最小值肯定是 i+1 时间复杂度位O(n) 肯定达不到面试官的要求
- 利用排序的特性,使用二分查找,时间复杂度位O(logn)
package com.lovedata.interview.N11_MinNumberInRotatedArray;
/**
* @author pengshuangbao
* @date 2021/2/9 11:29 AM
*/
public class MinNumberInRotatedArray {
/**
* 时间复杂度O(n)
*
* @return
*/
public int min(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
for (int i = 0; i < nums.length; i++) {
if (nums[i] > nums[i + 1]) {
return nums[i + 1];
}
}
return nums[0];
}
/**
* 时间复杂度O(logn)
*
* @return
*/
public int min1(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int low = 0;
int high = nums.length - 1;
int mid = 0;
while (nums[low] >= nums[high]) {
//循环的推出条件是,如果high-low=1,则表明两人已经要相遇了,则则最小的肯定是右边这个树
if (high - low == 1) {
mid = high;
break;
}
mid = low + (high - low) / 2;
// 有一种特殊情况,就是 low high mid 三个树都是一样的,则只能顺序查找了,退化
if (nums[mid] == nums[low] && nums[low] == nums[high]) {
return min(nums);
}
//第一种情况,如果这个mid>=low,则最小值tmd肯定是在后面,则low往后移动
if (nums[mid] >= nums[low]) {
low = mid;
} else if (nums[mid] <= nums[high]) {
// 第二种情况,如果这个mid<=high ,则最小值肯定在左边,或者就是他本身
//还有个情况要注意,要多考虑边界的情况,如果死循环了,则可能是因为边界没处理好
// 比如 这两个表,就是少了 = 导致一直不满足 而死循环了
high = mid;
}
}
return nums[mid];
}
public static void main(String[] args) {
MinNumberInRotatedArray minNumberInRotatedArray = new MinNumberInRotatedArray();
System.out.println(minNumberInRotatedArray.min(new int[]{2, 3, 0, 1}));
System.out.println(minNumberInRotatedArray.min1(new int[]{2, 3, 4, 1, 1}));
}
}
# 回溯法
蛮力法的升级版,它从解决问题的每一步所有可能选项里系统的选择一个可行的解决方案, 回溯法特别适合有多个步骤组成的问题,并且每个步骤有多个选项,当选择了一个后,就进入下一个,然后又面临很多选项
当选项都不能满足要求的时候,就要返回上一步,继续选择。
# 面试题12: 矩阵中的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。 例如下面矩阵
a b t g c f c s j d e h
包含一条字符串"bfce"的路径,但是矩阵中不包含"abfb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子
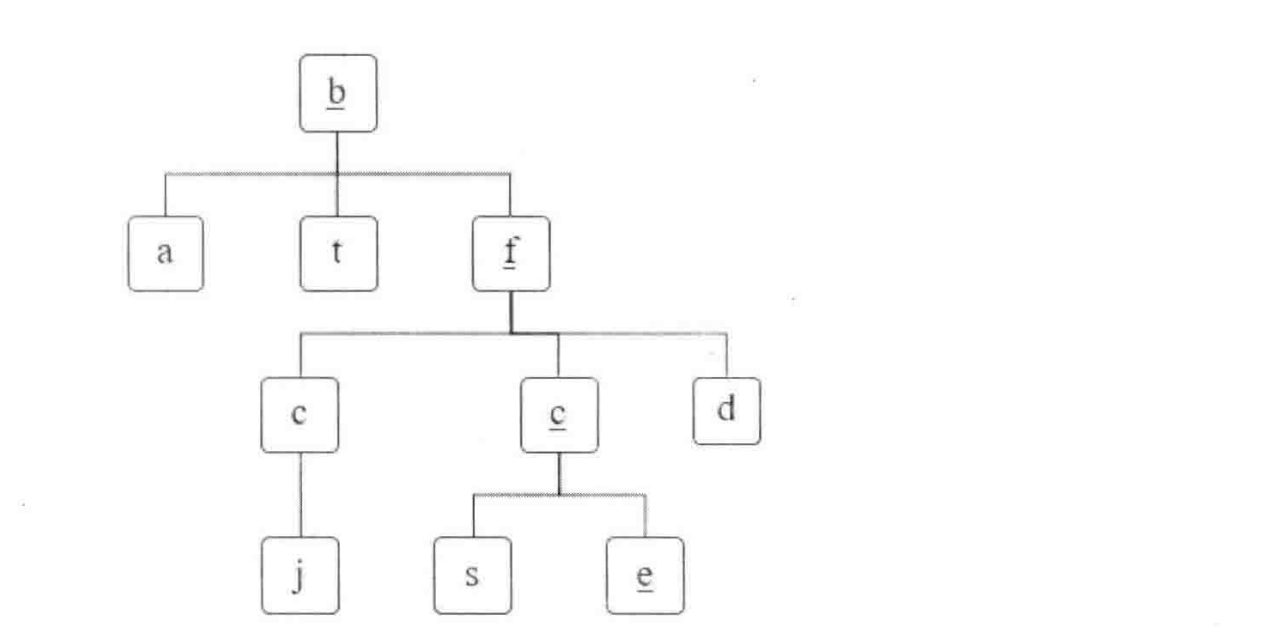
package com.lovedata.interview.N12_StringPathInMatrix;
/**
* @author pengshuangbao
* @date 2021/2/9 1:12 PM
*/
public class StringPathInMatrix {
public boolean hasPath(char[] matrix, int rows, int cols, char[] str) {
if (matrix == null || matrix.length == 0 || rows <= 0 || cols <= 0 || str == null || str.length == 0) {
return false;
}
//有一个数组,用于标示每一个点是否有访问过,因为已经访问过的,不能二次进入
boolean[] marked = new boolean[matrix.length];
//遍历这个矩阵的每一个字符,从左上角,一个个遍历
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
if (hasPathTo(matrix, rows, cols, row, col, str, 0, marked)) {
return true;
}
}
}
return false;
}
private boolean hasPathTo(char[] matrix, int rows, int cols, int row, int col, char[] str, int len, boolean[] marked) {
int index = row * cols + col;
//如果
// row 大于 rows
// col 大于 cols
// row < 0
// col < 0
// 矩阵的index处与str的 len 不相等
// 已经找过了
// 都是返回false
if (row > rows || row < 0 || col > cols || col < 0 || matrix[index] != str[len] || marked[index]) {
return false;
}
//如果正好这个长度和字符串的长度相同,则标示完全匹配
if (len == str.length - 1) {
return true;
}
//这个时候,说明还没匹配玩,虽然匹配到了,标示一下,继续往下
marked[index] = true;
//然后继续往下诏
//从上下左右四个方向找
// 四个方向上有没有可以到达下一个字符的路径,有任意一个方向可以就继续下一个字符的搜索
if (hasPathTo(matrix, rows, cols, row, col - 1, str, len + 1, marked) ||
hasPathTo(matrix, rows, cols, row - 1, col, str, len + 1, marked) ||
hasPathTo(matrix, rows, cols, row, col + 1, str, len + 1, marked) ||
hasPathTo(matrix, rows, cols, row + 1, col, str, len + 1, marked)) {
return true;
}
//回溯失败,标示上下左右都没找到,则当前这个点就废掉了,标示为false
marked[index] = false;
return false;
}
public static void main(String[] args) {
/**
* a b t g
* c f c s
* j d e h
*/
StringPathInMatrix stringPathInMatrix = new StringPathInMatrix();
System.out.println(stringPathInMatrix.hasPath("abtgcfcsjdeh".toCharArray(), 3, 4, "abf".toCharArray()));
}
}
# 面试题13:机器人的运动范围
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
这道题用通俗的话来讲就是:m行n列的所有方格中,有多少个满足行坐标和列坐标的数位之和小于等于门限值k的格子?
package com.lovedata.interview.N13_RobotMove;
/**
* @author pengshuangbao
* @date 2021/2/9 2:49 PM
*/
public class RobotMove {
public int movingCount(int rows, int cols, int threshold) {
if (rows <= 0 || cols <= 0 || threshold < 0) {
return 0;
}
boolean[] marked = new boolean[rows * cols];
return move(rows, cols, 0, 0, threshold, marked);
}
public int move(int rows, int cols, int row, int col, int threshold, boolean[] marked) {
int count = 0;
if (check(rows, cols, row, col, threshold, marked)) {
marked[row * cols + col] = true;
count = 1 + move(rows, cols, row - 1, col, threshold, marked)
+ move(rows, cols, row + 1, col, threshold, marked)
+ move(rows, cols, row, col + 1, threshold, marked)
+ move(rows, cols, row, col - 1, threshold, marked);
}
return count;
}
private boolean check(int rows, int cols, int row, int col, int threshold, boolean[] marked) {
// 验证条件
// row < rows
// col < cols
// row >=0
// col >=0
//marked 中没有标记过
//为数相加小于等于threshold
boolean check = false;
check = row < rows && col < cols && row >= 0 && col >= 0 && !marked[cols * row + col] && (digitSum(row) + digitSum(col)) <= threshold;
return check;
}
private int digitSum(int num) {
int sum = 0;
while (num > 0) {
sum += num % 10;
num /= 10;
}
return sum;
}
public static void main(String[] args) {
/**
* 0 1 2
* 3 4 6
* 6 7 8
*/
RobotMove robotMove = new RobotMove();
System.out.println(robotMove.movingCount(3, 3, 100));
}
}
# 动态规划与贪婪算法
如果是求一个问题的最优解(最小值或最大值),这个问题可以拆解成若干个子问题,子问题之间还有重叠的更小的问题,就可以考虑用动态规划。
使用动态规划之前 能否把大问题拆解成小问题,并且小问题也有最优解, 小问题的最优解组合在一起得到大问题的最优解。
# 四大特点
- 剪出的各段绳子乘机最大,也就是求一个问题的最优解
- 整体问题的最优解,是依赖各个子问题的最优解
- 大问题分成若干个小问题 这些小问题之间还有互相重叠的更小的问题
- 从上往下分析问题,从下往上解决问题
# 面试题14:剪绳子
给你一根长度为n的绳子,把绳子剪成m段(m、n都是整数且m > 1, n > 1),m段绳子的长度依然是整数,求m段绳子的长度乘积最大为多少?比如绳子长度为8,我们可以分成2段、3段、4段...8段,只有分成3段且长度分别是2、3、3时能得到最大乘积18
递归的思路

# 动态规划版本
要求大问题的最优解,可以将大问题分解成小问题,分解的小问题也有最优解,因此将小问题的最优解组合起来就能得到大问题的最优解。若将f(n)定义为将长度为n的绳子分成若干段后的各段长度的最大乘积(最优解),在剪第一刀时有n-1种剪法,可选择在0 < i < n处下刀;如在i处下刀,分成长度为i的左半绳子和长度为n - i的右半绳子,对于这两根绳子,定义最优解为f(i)和f(n-i),于是f(n) = max(f(i) * f(n-i)),即求出各种相乘可能中的最大值就是f(n)的最优解。这两根绳子又可以继续分下去,就这样从上到下的分下去,但是问题的解决得从下到上来。因为f(2)、f(3)的很好求:
- f(2) = 1,因为只能分成两半
- f(3) = 2,因为分成两段
2*1大于分成三段的1*1*1 - 然后根据这两个最优解求出f(4)、f(5)...直到f(n),每个f(i)的确定是通过遍历所有可能的相乘情况,从中选出乘积最大者。
package com.lovedata.interview.N14_CuttingRope;
/**
* @author pengshuangbao
* @date 2021/2/10 12:14 PM
* 给你一根长度为n的绳子,把绳子剪成m段(m、n都是整数且m > 1, n > 1)
* ,m段绳子的长度依然是整数,求m段绳子的长度乘积最大为多少?
* 比如绳子长度为8,我们可以分成2段、3段、4段...8段,只有分成3段且长度分别是2、3、3时能得到最大乘积18
*/
public class CuttingRope {
public int maxProductAfterCutting(int length) {
// 剪绳子 回溯算法
// 先从最小的,最简单的算出结果
if (length < 2) {
//如果为1,剪不了,不符合题意,直接返回
return 0;
}
if (length == 2) {
// 长度为2,只能剪出 1,1,乘机为1
return 1;
}
if (length == 3) {
// 长度为3, 能剪出 {2,1},{1,1,1} 前面的乘机为2大于后面的,所以返回2
return 2;
}
// 这样几个简单的就算出来了,即 f(1) = 0, f(2) = 1, f(3) = 2,继续往后算,就需要循环了
// 初始化一个数字,长度为 length+1,
// 因为到时候获取长度为 length 的时候,要使用 length下标,所以得+1
int[] products = new int[length + 1];
products[1] = 1;
products[2] = 2;
products[3] = 3;
// 这里 1 2 3 存的不是 f(1) f(2) f(3) 因为那些其实没必要存,直接存的长度
for (int i = 4; i <= length; i++) {
// 直接从4开始,前面的结果已经知道了,算到length
int max = 0;
//在求f(i) 之前 所有 f(j) 1<j<i 都已经算好了,比如
// i = 4 ,则 j 的取值区间为 1,2 都已经算好
// 为什么要除2,很好理解,从 1开始,到一半的时候,已经穷举了,过了一半,相当于又来了一遍了,没必要
for (int j = 1; j <= i / 2; j++) {
//第二轮循环 为了求 f(i) 需求求出所有的 f(j) * f(i-j)
//比如 i=4,有以下两种可能可能 {1,3},{2,2},其实还有一种 {1,1,2} 或者{1,1,1,1},但是明显前面的大
int product = products[j] * products[i - j];
if (product > max) {
max = product;
}
}
//直接把max赋值给i,因为这一轮已经对比算出,max就是所有可能中最大的了。
products[i] = max;
}
return products[length];
}
public static void main(String[] args) {
CuttingRope cuttingRope = new CuttingRope();
System.out.println(cuttingRope.maxProductAfterCutting(5));
}
}
对于长度为2或者3的绳子,可以直接返回答案。之后f(4)~f(n)的值存放在了products[4]~products[n]中,注意product[1]~products[3]中存放的不是f(1)~f(3),它们单纯地表示长度而已,作为求出
f(i),4 <= i <= n的辅助。最后得到的f(n)存放在products[n]中,直接返回即可。第二层中的for循环为了得到f(i),遍历了所有可能的乘积情况,将最大乘积赋予max。j <= i / 2是为了避免重复的相乘情况,比如i = 4时,只有2*2和1*3两种,3*1和1*3是同一种相乘情况,所以j只到i / 2 = 2即可枚举所有相乘情况。
# 位运算
把数字用二进制表示,对每一位上面的 0 1 坐运算

左移运算符 m<<n 表示把 m 左移 n 位 最左边的n位将会被丢弃 右边的n位补0

右移比较复杂点,分有符号数和无符号数,如果是无符号数只,直接在最边补0,如果是有符号数,则用数字的符号位补最左边的n位

# 二进制表
| 十进制 | 二进制 |
|---|---|
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
# 面试题15:二进制中1的个数
输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
# 错误版本,右移
/**
* 这个解法是错误的,负数回死循环
*
* @param num
* @return
*/
public int error(int num) {
int count = 0;
while (num != 0) {
if ((num & 1) == 1) {
count++;
}
num = num >> 1;
}
return count;
}
注意!上面的代码是错误的!对于非负数来说没有问题,但是当传入负数的时候,由于>>是带符号的右移,对于负数来说高位会以1补位,n永远也不会等于0,因此会出现无限循环。
在Java中右移分两种,一种是上面那样带符号的右移,用>>表示,如果数是正数高位以0补位,如果是负数高位以1补位;还有就是无符号的右移,用>>>表示,不论正负数,统统高位以0补位。因此只需改动将上述程序的>>改成>>>即可通过。
# 常规的正确版本
/**
*
* 正确的程序
* 不带符号的右移
* @param num
* @return
*/
public int numberOf1_2(int num) {
int count = 0;
while (num != 0) {
if ((num & 1) == 1) {
count++;
}
num = num >>> 1;
}
return count;
}
# 左移版本
上面的第一种错误解法会出现死循环,之所以出现,是因为改变了输入值本身。所以通过另外一个变量来左移实现
/**
* 左移的解法
*
* @param num
* @return
*/
public int numberOf1_1(int num) {
int count = 0;
int flag = 1;
while (flag != 0) {
if ((num & flag) != 0) {
count++;
}
flag = flag << 1;
}
return count;
}
# 更为巧妙的方法
/**
* 更为巧妙的解法
* 把一个数字减去一 ,发现它最右边的一个1编程0,如果右边还有0,则把所有的0变成了1
* 而左边的位保持不变 接下来把一个整数和 减去1之后的结果做 位与运算
* 相当于把最右边的1编程了0 举个例子
* 1100 (12) 减去1 为 1011
* 把1100 和 1011 做位与运算,则结果位1000,我们把1100最右边的1变成了0,刚好是1000
* 总结就是:把一个整数减去1,在和原来的数做位与运算,就会把最右边的1变成了0
* 那么有多少个1,做了多少次这样的运算就算出来了
*
* @param num
* @return
*/
public int numberOf1(int num) {
int count = 0;
while (num != 0) {
count++;
num = (num - 1) & num;
}
return count;
}
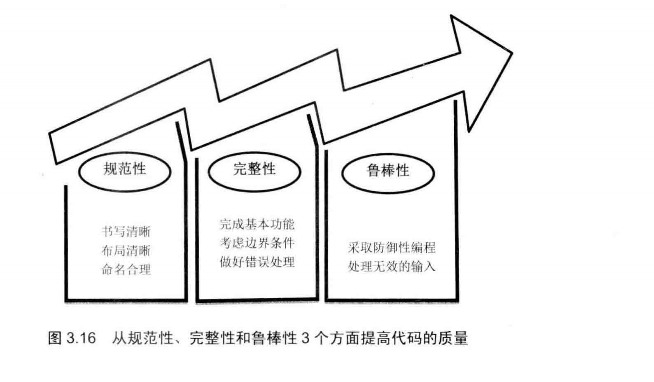
# 高质量代码
# 代码规范性
# 代码完整性
# 3个方面保证代码的完整性
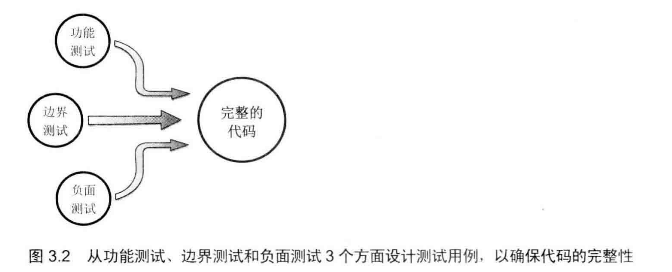
- 功能测试:正常的功能
- 边界测试: 边界值判断,最大数,最小数,循环的边界值,递归的终止边界值
- 负面测试: 各种错误输入
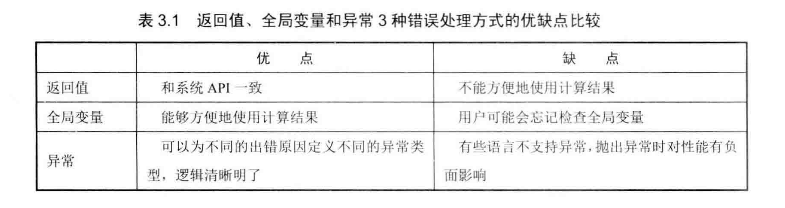
# 3种错误处理的方法
# 面试题16 -数值的整数次方
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。不得使用库函数直接实现,无需考虑大数问题。
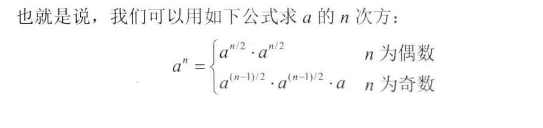
public class Power {
/**
* 非递归。推荐的做法,复杂度O(lg n)
*/
public double power(double base, int exponent) {
if (base == 0) {
return 0;
}
double result = 1.0;
int positiveExponent = Math.abs(exponent);
while (positiveExponent != 0) {
// positiveExponent & 1这句是判断奇数的
if ((positiveExponent & 1) == 1) {
result *= base;
}
base *= base;
// 右移1位等于除以2
positiveExponent = positiveExponent >> 1;
}
return exponent < 0 ? 1 / result : result;
}
public static void main(String[] args) {
Power power = new Power();
System.out.println(power.power(2, 4));
}
}
# 面试题17--打印从1到最大的n位十进制数
输入数字n,按顺序打印处1到最大的n位十进制数,比如输入3,则打印1~999之间的数
/**
* @author pengshuangbao
* @date 2021/2/20 11:45 AM
*/
public class Print1ToMaxOfNDigits {
/**
* 陷阱 这样没有考虑大数问题,超出了int类型的范围,就会报错
*/
public void print1ToMaxOfDigitsFault(int n) {
int number = 1;
int i = 0;
while (i++ < n) {
number *= 10;
}
for (int j = 1; j < number; j++) {
System.out.println(j);
}
}
public void print1ToMaxOfDigits(int n) {
if (n <= 0) {
return;
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < n; i++) {
sb.append('0');
}
while (stillIncrease(sb, n)) {
print(sb);
}
}
private void print(StringBuilder sb) {
//打印一个字符串,因为默认都是0,所以要先找到第一个不为0的位置
int start = sb.length();
for (int i = 0; i < sb.length(); i++) {
if (sb.charAt(i) != '0') {
start = i;
break;
}
}
if (start < sb.length()) {
System.out.println(sb.substring(start));
}
}
private boolean stillIncrease(StringBuilder sb, int n) {
int jinwei = 0;
for (int i = n - 1; i >= 0; i--) {
//首先要加上进为的数,从后面进上来的
//这里要-0,是因为char 转 int 要减去0,比如 char '0' 其实是标示为整数位48
int sum = sb.charAt(i) - '0' + jinwei;
//在个位上,要加1
if (i == n - 1) {
sum++;
}
//如果sum等于10,表示要进位
if (sum == 10) {
//如果当前的i==0了,还要进位,那就进不了啦,则溢出了
if (i == 0) {
return false;
} else {
//否则就把当前位设置位0,并进1
sb.setCharAt(i, '0');
jinwei = 1;
}
} else {
sb.setCharAt(i, (char) (sum + '0'));
break;
}
}
return true;
}
public static void main(String[] args) {
Print1ToMaxOfNDigits print1ToMaxOfNDigits = new Print1ToMaxOfNDigits();
print1ToMaxOfNDigits.print1ToMaxOfDigits(2);
}
}
# 剑指offer面试题18——删除链表的结点
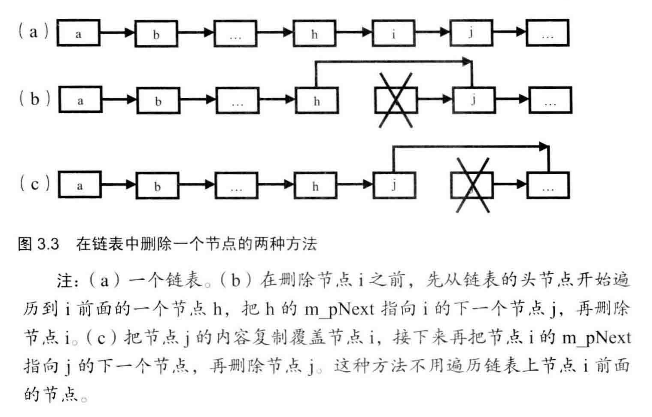
# 题目一—O(1)删除链表结点
给定单向链表的头指针和一个结点指针,定义一个函数在O(1)时间内删除该结点。假设要删除的结点确实在链表中。
/**
* @author pengshuangbao
* @date 2021/2/20 4:06 PM
*/
public class DeleteNodeInList {
private class Node {
int val;
Node next;
}
/**
* 将toBeDel的下一个结点j的值复制给toBeDel。然后将toBeDel指向j的下一个结点
*/
public void deleteNode(Node first, Node toBeDel) {
if (first == null || toBeDel == null) {
return;
}
// 要删除的不是最后一个结点
if (toBeDel.next != null) {
Node p = toBeDel.next;
toBeDel.val = p.val;
toBeDel.next = p.next;
// 是尾结点也是头结点
} else if (first == toBeDel) {
first = first.next;
// 仅仅是尾结点,即在含有多个结点的链表中删除尾结点
} else {
Node cur = first;
while (cur.next != toBeDel) {
cur = cur.next;
}
cur.next = null;
}
}
}
# 题目二——删除链表中的重复结点
在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。例如,链表1->2->3->3->4->4->5 处理后为 1->2->5
package com.lovedata.interview.N18_02_DeleteDuplicatedNode;
/**
* @author pengshuangbao
* @date 2021/2/20 4:24 PM
*/
public class DeleteDuplicatedNode {
public ListNode deleteDuplicateNode(ListNode head) {
if (head == null || head.next == null) {
return head;
}
//上一个节点,如果是头节点,则pre位null
ListNode pre = null;
//当前节点,从头节点开始遍历
ListNode cur = head;
while (cur != null && cur.next != null) {
//如果当前节点和下一个节点的值相同,则需要删除
if (cur.val == cur.next.val) {
int val = cur.val;
//找到下一个值不等于当前值的节点
while (cur != null && (cur.val == val)) {
cur = cur.next;
}
//一旦跳出循环,则当前节点就是不等于val的节点
//如果pre位null,则标示当前节点是头节点
if (pre == null) {
head = cur;
} else {
pre.next = cur;
}
} else {
//否则继续往下遍历
pre = cur;
cur = cur.next;
}
}
return head;
}
public static void main(String[] args) {
ListNode head = new ListNode(1);
ListNode next = new ListNode(2);
ListNode next1 = new ListNode(2);
ListNode next2 = new ListNode(3);
head.next = next;
next.next = next1;
next1.next = next2;
print(head);
DeleteDuplicatedNode deleteDuplicatedNode = new DeleteDuplicatedNode();
print(deleteDuplicatedNode.deleteDuplicateNode(head));
}
public static void print(ListNode node) {
ListNode cur = node;
while (cur != null) {
System.out.print(cur.val);
cur = cur.next;
}
System.out.println();
}
}
class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
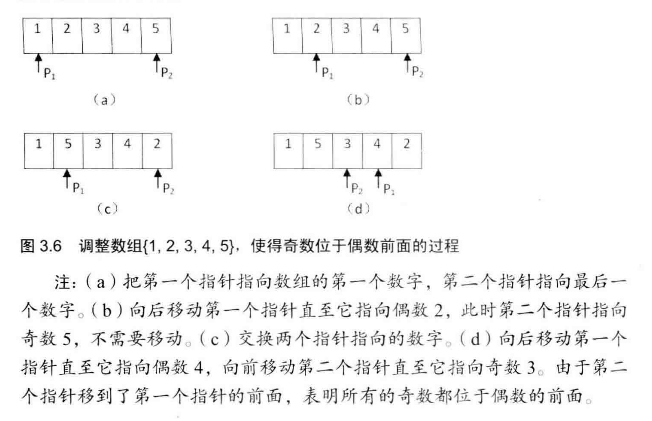
# 面试题21--调整数组的顺序使奇数位于偶数前面
输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
# 适合初级程序员
package com.lovedata.interview.N21_ReorderArray;
import java.util.function.Predicate;
import java.util.Arrays;
/**
* @author pengshuangbao
* @date 2021/2/20 5:05 PM
* 输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
*/
public class ReorderArray {
/**
* 第一种思路
* 搞一个辅助数组,遍历原始数组,碰到基数,先放进去,然后在遍历一次,存入偶数
*
* @param array
*/
public void reOrderArray(int[] array) {
if (array == null || array.length == 0) {
return;
}
// 一个指针,从左往右
int p = 0;
int[] temp = new int[array.length];
// 第一次遍历,存入奇数
for (int i = 0; i < array.length; i++) {
if (isOdd(array[i])) {
temp[p++] = array[i];
}
}
// 第二次遍历,存入偶数
for (int i = 0; i < array.length; i++) {
if (!isOdd(array[i])) {
temp[p++] = array[i];
}
}
//还原
for (int i = 0; i < array.length; i++) {
array[i] = temp[i];
}
}
/**
* 第二种思路:搞两个指针,一个初始指向第一个,一个初始指向数组的最后一个
* 第一个从前往后遍历,直到遇到一个偶数,第二个从后往前,直到遇到一个奇数
* 将偶数和奇数对掉
* 缺点:会改变奇数或者偶数之间的相对位置
*
* @param array
*/
public void reOrderArray1(int[] array, Predicate<Integer> predicate) {
if (array == null || array.length == 0) {
return;
}
int begin = 0;
int end = array.length - 1;
while (begin < end) {
//向前找,遇到一个偶数
while (begin < end && predicate.test(array[begin])) {
begin++;
}
while (begin < end && !predicate.test(array[end])) {
end--;
}
if (begin < end) {
int temp = array[begin];
array[begin] = array[end];
array[end] = temp;
}
}
}
private boolean isOdd(int i) {
return (i & 1) == 1;
}
public static void main(String[] args) {
ReorderArray reorderArray = new ReorderArray();
int[] array = {1, 2, 3, 4, 5};
reorderArray.reOrderArray(array);
System.out.println(Arrays.toString(array));
int[] array1 = {1, 2, 3, 4, 5};
reorderArray.reOrderArray1(array1, p -> reorderArray.isOdd(p));
System.out.println(Arrays.toString(array1));
}
}
# 代码鲁棒性
提高代码鲁棒性的方法是使用防御性编程。
多位几个“如果不。。。那么。。。”
不要按照固定的思维去思考,不能顺着别人的套路去做事,要有自己的套路,否则很容易被套路了。
# 面试题22-链表中倒数第k个结点
输入一个链表,输出该链表中倒数第k个结点。
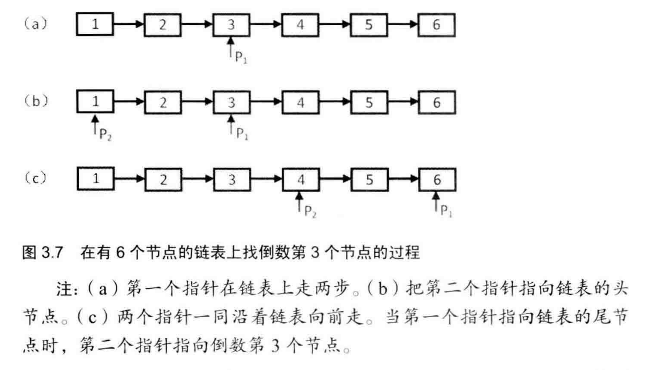
三种方式让程序崩溃,不够鲁棒

package com.lovedata.interview.N22_KthNodeFromEnd;
/**
* @author pengshuangbao
* @date 2021/2/20 5:59 PM
*/
public class KthNodeFromEnd {
public ListNode FindKthToTail(ListNode head, int k) {
if (head == null || k <= 0) {
return null;
}
ListNode a = head;
ListNode b = head;
//两个指针 第一个指针先移动k-1步
for (int i = 0; i < k - 1; i++) {
if (a.next == null) {
return null;
}
a = head.next;
}
//这个时候,两个指针一路往后移动,始终保持两个指针的举例是 k-1,
//当a到达链表尾部的时候,则b刚好是倒数第k个数
while (a.next != null) {
a = a.next;
b = b.next;
}
return b;
}
public static void main(String[] args) {
ListNode head = new ListNode(1);
ListNode next = new ListNode(2);
ListNode next1 = new ListNode(5);
ListNode next2 = new ListNode(3);
head.next = next;
next.next = next1;
next1.next = next2;
print(head);
KthNodeFromEnd kthNodeFromEnd = new KthNodeFromEnd();
System.out.println(kthNodeFromEnd.FindKthToTail(head, 2).val);
}
public static void print(ListNode node) {
ListNode cur = node;
while (cur != null) {
System.out.print(cur.val);
cur = cur.next;
}
System.out.println();
}
}
class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
# 面试题23--链表中环的入口结点
一个链表中包含环,请找出该链表的环的入口结点。

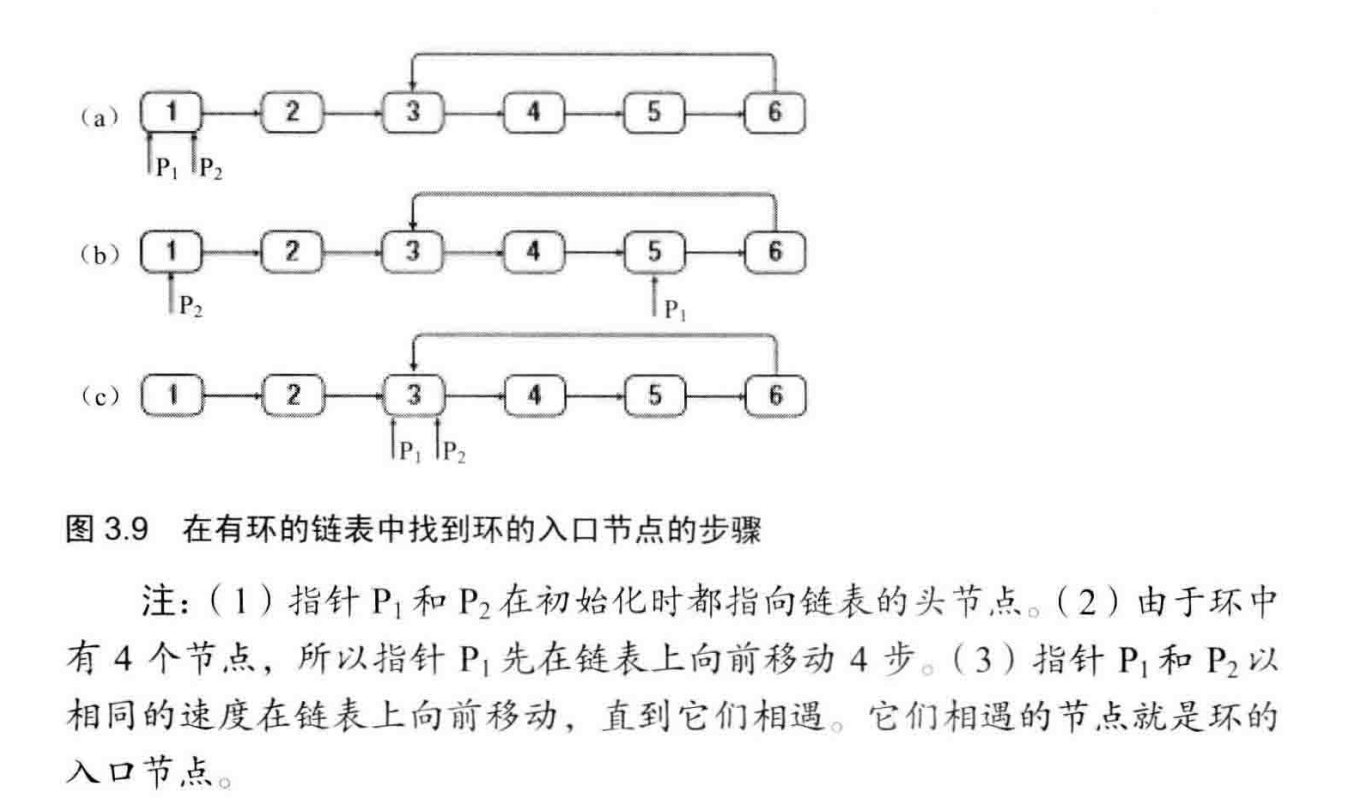
# 双指针法
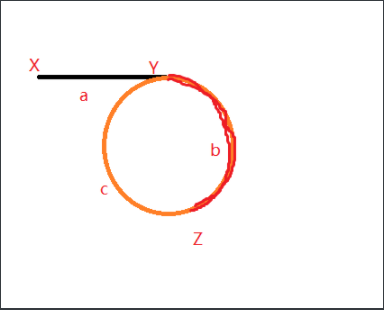
如下图,Y是环的入口结点,X是链表头结点。X、Y之间的步数为a。假设按照a -> b -> c ->b -> c...的顺序走。pFast走两步的同时pSlow走一步,最后他们一定会相遇。
为什么一定会相遇?试想操场跑步,你跑得快就能超出跑得慢的同学好多圈;同样地如果链表有环,pFast一定会和pSlow的距离逐渐缩小,直到相遇。(最好画画图加深理解)
假设pFast和pSlow在Z处相遇。他们相遇时,pFast走过的步数一定是pSlow的两倍,即有
$$S_{fast} = 2S_{slow}$$
假设相遇时pFast在环内转了k圈,则
$$a + k(b+c) + b = 2(a + b), k \ge 1$$
移项得:
$$a = (k-1)(b+c) + c, k \ge 1$$
上面的等式说明:X到Y的步数a等于从Z处开始在环内转k-1圈后,再从Z到Y的步数是一样的。现在将pFast移动到X,pSlow保持在Z处,两者同时每次走一步,pFast走a步,pSlow走(k-1)(b+c) + c步,它们刚好会在Y处相遇,由此找到了这个入口结点。
package com.lovedata.interview.N23_EntryNodeInListLoop;
import java.util.HashSet;
import java.util.Objects;
import java.util.Set;
/**
* @author pengshuangbao
* @date 2021/2/22 11:47 AM
*/
public class EntryNodeInListLoop {
/**
* @param head 链表头节点
* @return 环的入口
*/
public ListNode entryNodeOfLoop(ListNode head) {
if (head == null || head.next == null) {
return null;
}
ListNode fast = head;
ListNode slow = head;
//因为fast走的快,所以,一定要判断fast不为空的情况,
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
// 如果有环,则一定回相遇,这是肯定的
if (slow == fast) {
// 这个时候,就遇到了环,因为相遇了,呵呵
// 然后fast从头开始跑
fast = head;
// 再次相遇,则肯定是在环的入口那里相遇了。
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
return null;
}
public static void main(String[] args) {
ListNode head = new ListNode(1);
ListNode next = new ListNode(2);
ListNode next1 = new ListNode(5);
ListNode next2 = new ListNode(3);
head.next = next;
next.next = next1;
next1.next = next2;
next2.next = next;
//这个时候,环的入口就是next 2
EntryNodeInListLoop entryNodeInListLoop = new EntryNodeInListLoop();
System.out.println(entryNodeInListLoop.entryNodeOfLoop(head).val);
}
}
class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
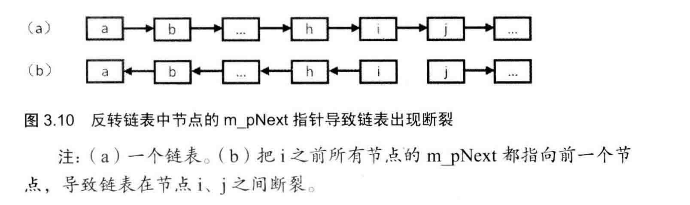
# 面试题24--反转链表
输入一个链表的头结点,反转链表后,并返回反转链表的头结点。
package com.lovedata.interview.N24_ReverseList;
/**
* @author pengshuangbao
* @date 2021/2/22 2:12 PM
*/
public class ReverseList {
public ListNode reverseList(ListNode head) {
ListNode reverseHead = null;
ListNode pre = null;
ListNode cur = head;
while (cur != null) {
ListNode next = cur.next;
if (next == null) {
reverseHead = cur;
}
cur.next = pre;
pre = cur;
cur = next;
}
return reverseHead;
}
public static void main(String[] args) {
ListNode head = new ListNode(1);
ListNode next = new ListNode(2);
ListNode next2 = new ListNode(3);
head.next = next;
next.next = next2;
print(head);
print(new ReverseList().reverseList(head));
}
public static void print(ListNode node) {
ListNode cur = node;
while (cur != null) {
System.out.print(cur.val);
cur = cur.next;
}
System.out.println();
}
}
class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
# 面试题25--合并两个有序链表
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
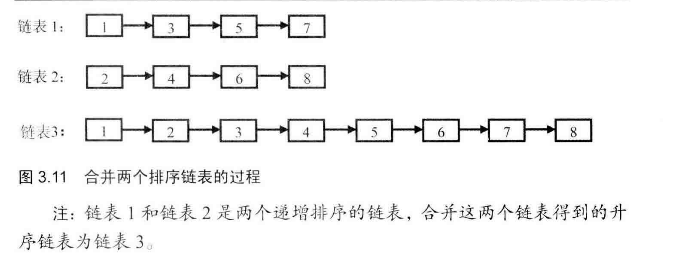
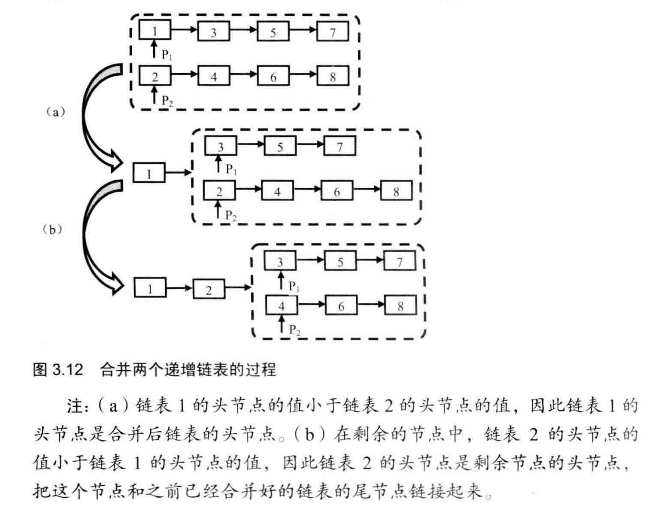

典型的递归的过程。
package com.lovedata.interview.N25_MergeSortedLists;
/**
* @author pengshuangbao
* @date 2021/2/22 2:31 PM
*/
public class MergeSortedLists {
public ListNode merge(ListNode head1, ListNode head2) {
if (head1 == null) {
return head2;
}
if (head2 == null) {
return head1;
}
ListNode pHead;
if (head1.val < head2.val) {
pHead = head1;
pHead.next = merge(head1.next, head2);
} else {
pHead = head2;
pHead.next = merge(head1, head2.next);
}
return pHead;
}
public static void print(ListNode node) {
ListNode cur = node;
while (cur != null) {
System.out.print(cur.val);
cur = cur.next;
}
System.out.println();
}
public static void main(String[] args) {
ListNode head = new ListNode(1);
ListNode next = new ListNode(4);
ListNode next2 = new ListNode(6);
head.next = next;
next.next = next2;
print(head);
ListNode head_2 = new ListNode(1);
ListNode next_2 = new ListNode(3);
ListNode next2_2 = new ListNode(5);
head_2.next = next_2;
next_2.next = next2_2;
print(head_2);
print(new MergeSortedLists().merge(head, head_2));
}
}
class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
# 面试题26--树的子结构
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
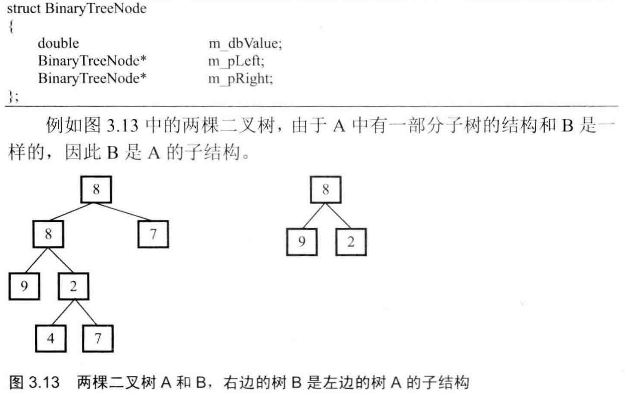
- 第一步:在树A种找到和树B的根节点的值一样的节点R
- 第二部:判断树A种以R为根节点的子树是不是包含和树B一样的结构
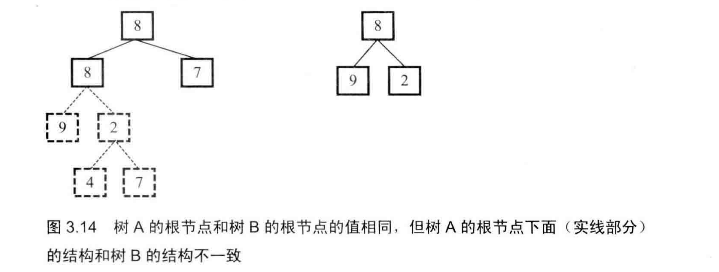
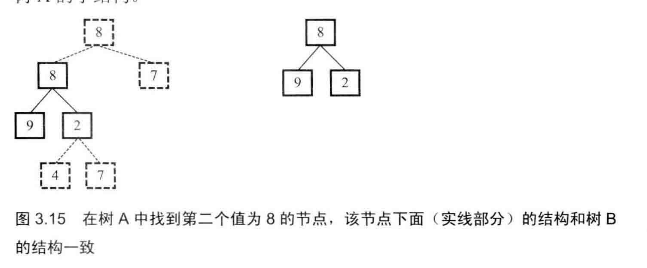
这就是对二叉树的遍历,一般使用递归,因为比较简洁,也可以用循环。
package com.lovedata.interview.N26_SubstructureInTree;
import utils.TreeNode;
import utils.TreeOperation;
/**
* @author pengshuangbao
* @date 2021/2/22 2:56 PM
* 输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
*/
public class SubstructureInTree {
public boolean hasSubTree(TreeNode node1, TreeNode node2) {
boolean result = false;
if (node1 == null || node2 == null) {
return false;
}
if (node1.val == node2.val) {
result = doseTree1HaveTree2(node1, node2);
}
if (!result) {
result = hasSubTree(node1.left, node2);
}
if (!result) {
result = hasSubTree(node1.right, node2);
}
return result;
}
private boolean doseTree1HaveTree2(TreeNode node1, TreeNode node2) {
// node2到达叶子结点的左右子结点了都还相等,说明是树1的子结构
if (node2 == null) {
return true;
}
//// 如果node2没有到叶子结点的左右子结点,而node1先到了说明树2比树1还大,返回false
if (node1 == null) {
return false;
}
if (node1.val != node2.val) {
return false;
}
return doseTree1HaveTree2(node1.left, node2.left) && doseTree1HaveTree2(node1.right, node2.right);
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
node2.right = node5;
node2.left = node6;
TreeOperation.show(roo1);
TreeNode roo1_2 = new TreeNode(3);
TreeNode node1_2 = new TreeNode(6);
TreeNode node2_2 = new TreeNode(5);
roo1_2.left = node1_2;
roo1_2.right = node2_2;
TreeOperation.show(roo1_2);
System.out.println(new SubstructureInTree().hasSubTree(roo1, roo1_2));
}
}
# 解决面试题的思路
解答面试题的时候,要先有一个思路,不要上来就作答
比如要先理清是什么,为什么,怎么弄,多问问why,what,不要一上来就搞!!!!
# 画图让抽象问题形象化
帮助自己分析推理的常用手段
画图让抽象问题具体化,形象化,通过画几个图,说不定就能找到规律并作出解答
二叉树,二维数组,都可以用画图来帮忙分析
对面试官,也可以通过画图来讲解,一边画图,一边讲解。
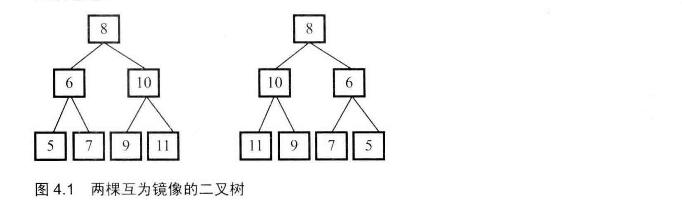
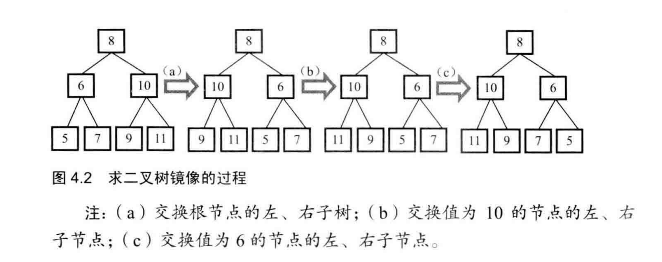
# 面试题27-二叉树的镜像
操作给定的二叉树,将其变换为原二叉树的镜像。
package com.lovedata.interview.N27_MirrorOfBinaryTree;
import utils.TreeNode;
import utils.TreeOperation;
/**
* @author pengshuangbao
* @date 2021/2/22 4:04 PM
* 面试题27-操作给定的二叉树,将其变换为原二叉树的镜像。
*/
public class MirrorOfBinaryTree {
public void mirrorOfBinaryTree(TreeNode head) {
//如果是空,则返回
if (head == null) {
return;
}
//如果左右子节点都是null,则返回
if (head.left == null && head.right == null) {
return;
}
// 将左右子节点
TreeNode temp = head.left;
head.left = head.right;
head.right = temp;
//然后继续镜像左右子节点
if (head.left != null) {
mirrorOfBinaryTree(head.left);
}
if (head.right != null) {
mirrorOfBinaryTree(head.right);
}
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
node2.right = node5;
node2.left = node6;
TreeOperation.show(roo1);
new MirrorOfBinaryTree().mirrorOfBinaryTree(roo1);
TreeOperation.show(roo1);
}
}
# 面试题28-对称的二叉树
请实现一个函数,用来判断一颗二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
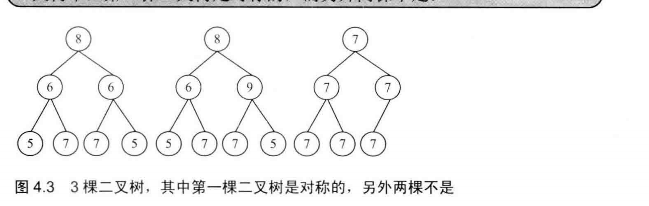
可以通过比较二叉树的前序遍历序列和对称谦虚遍历序列来判断二叉树是不是对称的,如果两个序列是一样的,则是对称的

package com.lovedata.interview.N28_SymmetricalBinaryTree;
import utils.TreeNode;
import utils.TreeOperation;
/**
* @author pengshuangbao
* @date 2021/2/22 5:05 PM
* 面试题28-对称的二叉树
*
* 请实现一个函数,用来判断一颗二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
*/
public class SymmetricalBinaryTree {
public boolean isSummertrical(TreeNode root) {
return isSummertrical(root, root);
}
public boolean isSummertrical(TreeNode root1, TreeNode root2) {
//两个都为NULl,才是返回true
if (root1 == null && root2 == null) {
return true;
}
//如果只是其中一个为空,则肯定不对称啦
if (root1 == null || root2 == null) {
return false;
}
if (root1.val != root2.val) {
// 如果值不相同,那肯定也是false
return false;
}
// 用左节点 和 右节点对比
// 第一个节点的左节点和第二个节点的右节点相比
// 第一个节点的右节点和第二个节点的左节点相比
// 两个都满足,则对称
return isSummertrical(root1.left, root2.right)
&& isSummertrical(root1.right, root2.left);
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(2);
roo1.left = node1;
roo1.right = node2;
TreeOperation.show(roo1);
System.out.println(new SymmetricalBinaryTree().isSummertrical(roo1));
}
}
# 面试题29--顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字 1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.


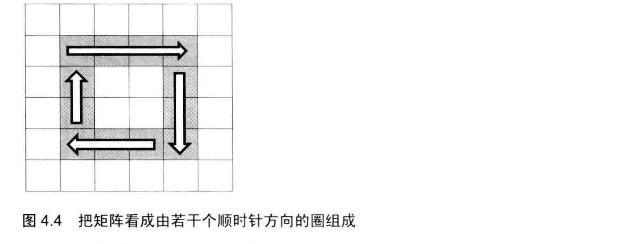
对于这种问题,从最简单的开始分析,比如 两行两列 三行三列。画一画图就清洗了
package com.lovedata.interview.N29_PrintMatrix;
/**
* @author pengshuangbao
* @date 2021/2/22 7:39 PM
*/
public class PrintMatrix {
public void printMatrix(int[][] numbers, int rows, int columns) {
if (numbers == null || numbers.length == 0) {
return;
}
if (rows <= 0 || columns <= 0) {
return;
}
// 从左上角的坐标为0开始
int start = 0;
while (rows > 2 * start && columns > 2 * start) {
printInCicle(numbers, rows, columns, start);
start++;
}
}
private void printInCicle(int[][] numbers, int rows, int columns, int start) {
//打印四步 -> ⬇️ <-️ ⬆️
// 要有一个打印的范围 比如 截止横坐标,截止纵坐标
int endX = columns - start - 1;
int endY = rows - start - 1;
//第一步肯定都回打印的
for (int i = start; i <= endX; i++) {
int number = numbers[start][i];
System.out.println(number);
}
// 第二步 从上到下打印
if (start < endY) {
// 这里要加一,否则回打印重复
for (int i = start + 1; i <= endY; i++) {
int number = numbers[i][endX];
System.out.println(number);
}
}
// 第三部 从右到左边打印
if (start < endX && start < endY) {
// 这里要减去1,否则要打印重复
for (int i = endX - 1; i >= start; i--) {
int number = numbers[endY][i];
System.out.println(number);
}
}
// 第四步 从下到上打印
if (start < endY - 1 && start < endX) {
// 这里要 减去一,否则,回打印重复
for (int i = endY - 1; i >= start + 1; i--) {
int number = numbers[i][start];
System.out.println(number);
}
}
}
public static void main(String[] args) {
/**
* 1 2 3 5
* 4 5 6 3
* 7 8 9 5
* 9 5 4 3
*/
int[][] numbers = {{1, 2, 3, 5}, {4, 5, 6, 3}, {7, 8, 9, 5}, {9, 5, 4, 3}};
new PrintMatrix().printMatrix(numbers, 4, 4);
}
}
# 举例让抽象问题具体化
使用举例模拟的方法思考分析复杂的问题
当难以看出规律的时候,使用一两个简单的例子来模拟操作的过程
举例还能保证代码的质量,写完代码之后,搞几个简单例子验证一下。
# 面试题30--包含min方法的栈
定义栈的数据结构,请在该类型中实现一个能够得到栈最小元素的min函数。要求push、pop、min方法的时间复杂度都为O(1)
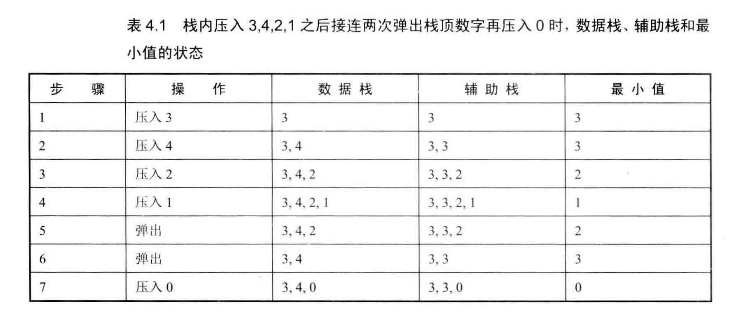
有些很容易想到的方法:比如每次想获得栈中的最小元素,将栈中所有元素复制到另一个数据结构中(比如List),然后对这个列表排序可以很简单地得到最小值。但时间复杂度肯定就不是O(1)了。
或者设置一个全局变量min,每次push都和当前最小值比较,如果更小就更新min,否则min不变。但是这种方法有个问题:要是pop出栈的元素正好就是这个min呢,那新的min是多少?我们很难得知,所以另辟蹊径。考虑到要求我们用O(1)的时间复杂度。可以考虑用空间换时间,试试使用辅助空间。
定义一个栈stackMin,专门用于存放当前最小值。
- 存放数据的stack存入当前元素,如果即将要存入的元素比当前最小元素还小,stackMin存入这个新的最小元素;否则,stackMin将当前最小元素再次存入。
- stack出栈时,stackMin也出栈。
反正就是入栈时,两个栈都有元素入栈;出栈时,两个栈都弹出一个元素。这两个栈总是同步进出栈的。
/**
* @author pengshuangbao
* @date 2021/2/23 10:21 AM
*/
public class MinInStack {
private LinkedList<Integer> stack = new LinkedList<>();
private LinkedList<Integer> minStack = new LinkedList<>();
public void push(Integer value) {
stack.push(value);
minStack.push(minStack.isEmpty() || value < minStack.peek() ? value : minStack.peek());
}
public Integer pop() {
if (stack.isEmpty()) {
throw new RuntimeException("stack is empty!");
}
minStack.pop();
return stack.pop();
}
public Integer min() {
if (minStack.isEmpty()) {
throw new RuntimeException("stack is empty!");
}
return minStack.peek();
}
}
# 面试题31--栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列 (注意:这两个序列的长度是相等的)
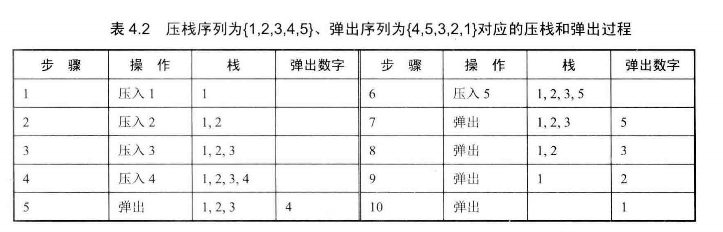
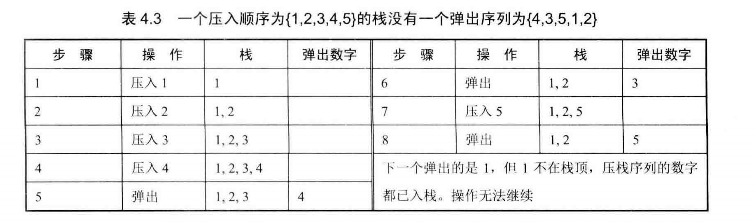
假如入栈顺序是[1, 2, 3, 4, 5]举个出栈顺序正确的例子[4, 5, 3, 2, 1]:
| 操作 | 辅助栈 | 出栈 |
|---|---|---|
| 压入1 | 1 | |
| 压入2 | 1, 2 | |
| 压入3 | 1, 2, 3 | |
| 压入4 | 1, 2 ,3 ,4 | |
| 弹出4 | 1,2 ,3 | 4 |
| 压入5 | 1,2, 3 ,5 | |
| 弹出5 | 1, 2, 3 | 5 |
| 弹出3 | 1,2 | 3 |
| 弹出2 | 1 | 2 |
| 弹出1 | 1 |
再举个错误的出栈顺序的例子[4,3,5,1,2]
| 操作 | 辅助栈 | 出栈 |
|---|---|---|
| 压入1 | 1 | |
| 压入2 | 1, 2 | |
| 压入3 | 1, 2, 3 | |
| 压入4 | 1, 2 ,3 ,4 | |
| 弹出4 | 1,2 ,3 | 4 |
| 弹出3 | 1, 2 | 3 |
| 压入5 | 1, 2, 5 | |
| 弹出5 | 1, 2 | 5 |
| 弹出2 | 2 | |
| 弹出1 | 1 |
package com.lovedata.interview.StackPushPopOrder;
import java.util.LinkedList;
/**
* @author pengshuangbao
* @date 2021/2/23 10:45 AM
*/
public class StackPushPopOrder {
public boolean isPushPopOrder(int[] push, int[] pop) {
if (push == null || push.length == 0 || pop == null || pop.length == 0) {
return false;
}
// 需要有一个辅助队列,来模拟入栈操作
LinkedList<Integer> stack = new LinkedList<Integer>();
// 需要一个指针
int index = 0;
// 根据入栈序列,模拟入展,一直往里加,直到到达第一个出栈元素匹配的时候
for (int i = 0; i < push.length; i++) {
//这里入栈
stack.push(push[i]);
// 这里拿栈顶和pop序列对比,如果匹配,则出栈,继续pop往后对比,如果没有匹配的,则继续入栈,如果有,则出栈
while (!stack.isEmpty() && pop[index] == stack.peek()) {
stack.pop();
index++;
}
}
// 最后模拟栈为空,则表示可以匹配
return stack.isEmpty();
}
public static void main(String[] args) {
System.out.println(new StackPushPopOrder().isPushPopOrder(new int[]{1, 2, 3, 4, 5}, new int[]{4, 5, 3, 2, 1}));
}
}
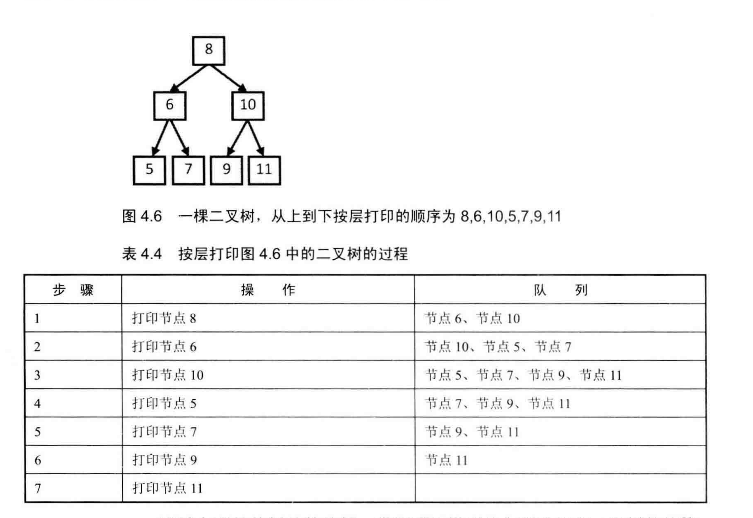
# 面试题32--从上到下打印二叉树
题目一: 不分行,从上往下打印出二叉树的每个节点,同层节点从左至右打印。即层序遍历
# 不分行,层序遍历
/**
* @author pengshuangbao
* @date 2021/2/23 11:42 AM
*
* 不分行,从上往下打印出二叉树的每个节点,同层节点从左至右打印。即层序遍历
*/
public class PrintTreeFromTopToBottom {
public ArrayList<Integer> printFromTopToBottom(TreeNode root) {
ArrayList<Integer> list = new ArrayList<Integer>();
if (root == null) {
return list;
}
Queue<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode poll = queue.poll();
list.add(poll.val);
if (poll.left != null) {
queue.offer(poll.left);
}
if (poll.right != null) {
queue.offer(poll.right);
}
}
return list;
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
node2.right = node5;
node2.left = node6;
TreeOperation.show(roo1);
System.out.println(new PrintTreeFromTopToBottom().printFromTopToBottom(roo1));
}
}
# 分行打印
package com.lovedata.interview.N32_02_PrintTreesInLines;
import java.util.LinkedList;
import com.lovedata.interview.N32_01_PrintTreeFromTopToBottom.PrintTreeFromTopToBottom;
import utils.TreeNode;
import utils.TreeOperation;
/**
* @author pengshuangbao
* @date 2021/2/23 11:51 AM
* 分行打印
*/
public class PrintTreesInLines {
public void printTreesInLines(TreeNode treeNode) {
if (treeNode == null) {
return;
}
LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
queue.offer(treeNode);
// 思路根上面是一样的, 但是需要辨别,什么时候一行结束了
// 需要两个变量,一个来标示当前行还有多少个没有打印,如果为0,则表示应该换行了
int currentLineToBePrint = 1;
// 下一行有多少个需要打印,这个变量的作用,是用来在换行的时候赋予到 currentLineToBePrint ,还是用来判断是否要换行的
int nextLevel = 0;
while (!queue.isEmpty()) {
TreeNode poll = queue.poll();
System.out.print(poll.val + " ");
currentLineToBePrint--;
if (poll.left != null) {
queue.offer(poll.left);
nextLevel++;
}
if (poll.right != null) {
queue.offer(poll.right);
nextLevel++;
}
if (currentLineToBePrint == 0) {
System.out.println();
currentLineToBePrint = nextLevel;
nextLevel = 0;
}
}
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
node2.right = node5;
node2.left = node6;
TreeOperation.show(roo1);
new PrintTreesInLines().printTreesInLines(roo1);
}
}
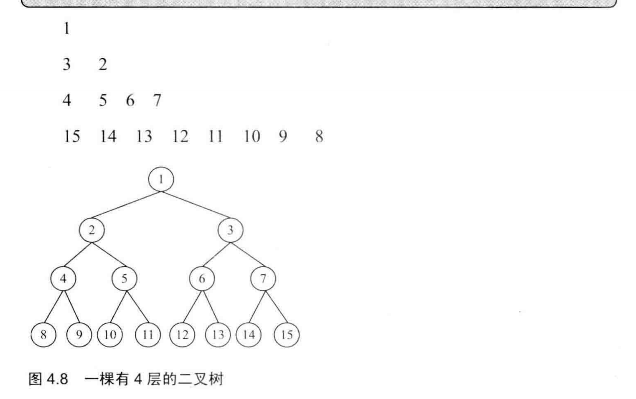
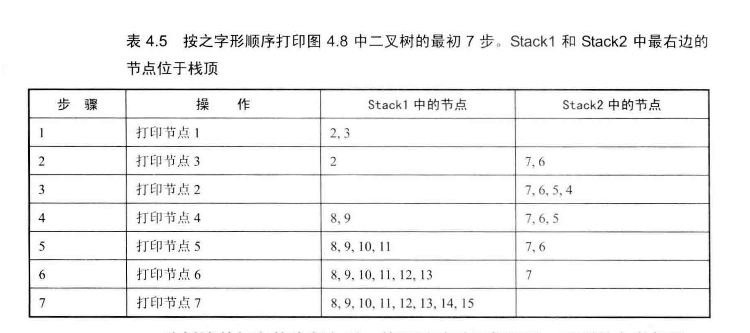
# Z字形打印二叉树
举个例子,下面的二叉树,打印顺序是1 3 2 4 5 6 7
1
/ \
2 3
/ \ / \
4 5 6 7
package com.lovedata.interview.N32_03_PrintTreesInZigzag;
import com.lovedata.interview.N32_01_PrintTreeFromTopToBottom.PrintTreeFromTopToBottom;
import utils.TreeNode;
import utils.TreeOperation;
import java.util.LinkedList;
/**
* @author pengshuangbao
* @date 2021/2/23 2:41 PM
* Z字形打印二叉树
* 举个例子,下面的二叉树,打印顺序是1 3 2 4 5 6 7
* 1
* / \
* 2 3
* / \ / \
*4 5 6 7
*/
public class PrintTreesInZigzag {
public void printTreesInZigzag(TreeNode root) {
if (root == null) {
return;
}
// 使用两个栈,栈是先进后出
// 当是偶数层的时候,从右往左打印,所以需要从左往右放入
// 奇数层相反
// 偶数栈,当前层是奇数的时候,
LinkedList<TreeNode> stackOdd = new LinkedList<>();
// 奇数栈, 当前层是偶数的时候,
LinkedList<TreeNode> stackEven = new LinkedList<>();
// 只要两个栈有一个不为空,循环继续
stackOdd.push(root);
while (!stackOdd.isEmpty() || !stackEven.isEmpty()) {
//当奇数层不为空的时候,则当前是奇数层
if (!stackOdd.isEmpty()) {
while (!stackOdd.isEmpty()) {
//下一层是偶数,则需要从左往右放入
TreeNode node = stackOdd.pop();
System.out.print(node.val + " ");
if (node.left != null) {
stackEven.push(node.left);
}
if (node.right != null) {
stackEven.push(node.right);
}
}
} else {
// 当奇数栈为空了,则就是偶数栈了
while (!stackEven.isEmpty()) {
TreeNode node = stackEven.pop();
System.out.print(node.val + " ");
// 下一层是奇数栈,则需要从右往左放入了
if (node.right != null) {
stackOdd.push(node.right);
}
if (node.left != null) {
stackOdd.push(node.left);
}
}
}
}
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
node2.right = node5;
node2.left = node6;
TreeOperation.show(roo1);
new PrintTreesInZigzag().printTreesInZigzag(roo1);
}
}
# 面试题33--二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
注意是二叉搜索(查找)树,特点是父结点的左子树都比父结点小,父结点的右子树都比父结点大。因此其后序遍历的序列有一定的规律:
- 序列最后一位必然是树的根结点;
- 序列前部分是根结点的左子树,后部分是根结点的右子树;具体来说:将序列各个元素和和序列最后一位的根结点比较,序列前部分都小于根结点的值,这部分子序列是左子树;序列后部分的值都大于根结点,这部分子序列是右子树;
- 前序:上左右
- 中序:左上右
- 后续:左右上
其实就是找规律的过程, 比如 5 7 6 9 11 10 8 最后一个8肯定是根节点,前面的分两个序列,左边的都是小于8的,右边的都是大于八的,所以找到 5 7 6 都是小于8的,7 11 10 都是大于8的 这一部分温和,继续下面的子树。比如 6 时根节点, 5 时左节点, 7 时右节点,是吻合的哟。
package com.lovedata.interview.N33_SquenceOfBST;
/**
* @author pengshuangbao
* @date 2021/2/23 3:20 PM
* ### 二叉搜索树的后序遍历序列
* <p>
* 输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
*/
public class SquenceOfBST {
public boolean verifySquenceOfBST(int[] sequence) {
if (sequence == null || sequence.length == 0) {
return false;
}
return isSearchBST(sequence, 0, sequence.length - 1);
}
/**
* 其实就是找规律的过程, 比如 5 7 6 9 11 10 8 最后一个8肯定是根节点,前面的分两个序列,左边的都是小于8的,
* 右边的都是大于八的,所以找到 5 7 6 都是小于8的,7 11 10 都是大于8的 这一部分温和,继续下面的子树。比如 6 时根节点, 5 时左节点, 7 时右节点,是吻合的哟。
* 7 4 6 5 肯定是不吻合的
*
* @param sequence
* @param begin
* @param end
* @return
*/
public boolean isSearchBST(int[] sequence, int begin, int end) {
// begin比end大说明上层结点没有左子树或者右子树,begin == end说明该本层结点没有子树,无需比较了
// 这两种情况都应该返回true
if (begin > end) {
return true;
}
//拿到根节点,根节点肯定是最后一个
int root = sequence[end];
// 寻找第一个大于 root的点,则前面的都是左子树
int i = begin;
// 找到第一个比
while (sequence[i] < root) {
i++;
}
//拿到分界点
int bondary = i;
while (i < end) {
// 如果右边子树有比根节点小的,肯定就是不行的呢
if (sequence[i] < root) {
return false;
}
i++;
}
// 继续查找左右子树
return isSearchBST(sequence, begin, bondary - 1) && isSearchBST(sequence, bondary, end - 1);
}
public static void main(String[] args) {
System.out.println(new SquenceOfBST().verifySquenceOfBST(new int[]{5, 7, 6, 9, 11, 10, 8}));
System.out.println(new SquenceOfBST().verifySquenceOfBST(new int[]{7, 4, 6, 5}));
}
}
# 面试题34--二叉树中和为某一值的路径
输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

很自然的想法是每条路径都和目标值比较,如果相同就将这条路径存入一个集合中,本质上是个深度优先搜索。
package com.lovedata.interview.N34_PathInTree;
import utils.TreeNode;
import utils.TreeOperation;
import java.lang.reflect.Array;
import java.util.ArrayList;
/**
* @author pengshuangbao
* @date 2021/2/23 4:21 PM
*/
public class PathInTree {
public ArrayList<ArrayList<Integer>> findPath(TreeNode root, int target) {
ArrayList<ArrayList<Integer>> res = new ArrayList<>();
ArrayList<Integer> path = new ArrayList<>();
// 传入target,每到一个路径,则减去这个路径的一个值,直到叶子节点,在做对比
preOrder(root, res, path, target);
return res;
}
private void preOrder(TreeNode root, ArrayList<ArrayList<Integer>> res, ArrayList<Integer> path, int target) {
if (root == null) {
return;
}
// 先把根节点添加到路径中
path.add(root.val);
//到一个节点,值减去节点的值
target -= root.val;
// 只有在叶子结点处才判断是否和目标值相同,若相同加入列表中
if (root.left == null && root.right == null) {
// 如果减去的值刚好等于0,则表示路径吻合,将路径加入到结果中去
if (target == 0) {
//这里要new一个Arraylist,不能直接添加path
//path是对象,后面还会操作的
res.add(new ArrayList<>(path));
}
}
// 如果不是叶子节点,继续下遍历,先遍历左边后右边
// 因为当前值已经减去了root.val,所以继续往下,左右传入的target都是一样的
preOrder(root.left, res, path, target);
preOrder(root.right, res, path, target);
// 当左右都遍历完之后,则当前root的递归完成,要继续往上,往上的话,target就要加上root.val
//模拟节点出战
path.remove(path.size() - 1);
target += root.val;
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
node2.right = node5;
node2.left = node6;
TreeOperation.show(roo1);
System.out.println(new PathInTree().findPath(roo1, 9));
}
}
# 分解让复杂问题简单化
各个击破,把强大的敌人分割开来,集中优势兵力各个击破,一次战胜强大的敌人很困难,但是战胜小股敌人久容易多了。
分步骤,每一个步骤解决一个小问题。
计算机领域有一个分治法,分而治之的方法,通常分而治之的方法都是用递归来实现
# 面试题35--复杂链表的复制
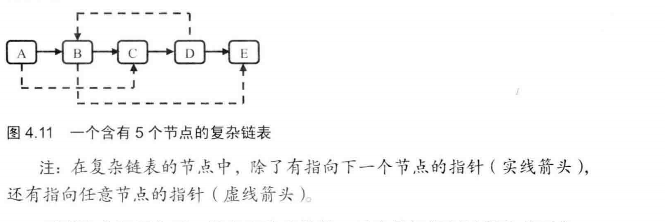
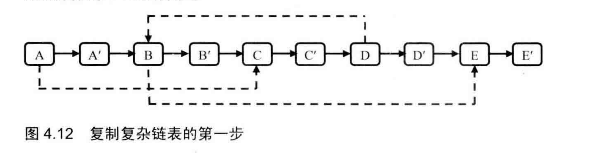
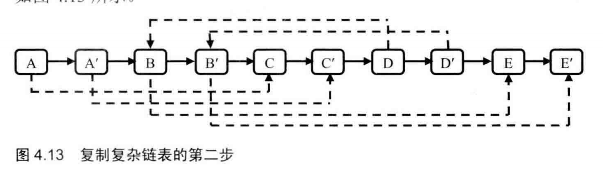
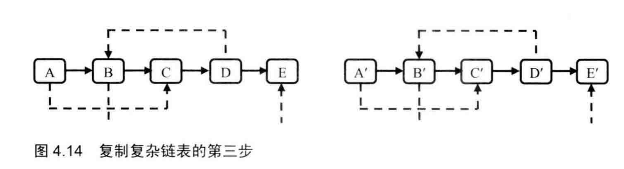
输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针指向任意一个节点),返回结果为复制后复杂链表的head。(注意,输出结果中请不要返回参数中的节点引用,否则判题程序会直接返回空)
package com.lovedata.interview.N35_CopyComplexList;
import java.util.Random;
import java.util.Random;
/**
* @author pengshuangbao
* @date 2021/2/23 5:39 PM
*/
public class CopyComplexList {
public RandomListNode clone(RandomListNode root) {
//第一步 复制节点
copyNode(root);
//第二步 设置随机节点
setRandomNode(root);
//第三步 拆分节点
return splitNode(root);
}
private RandomListNode splitNode(RandomListNode root) {
RandomListNode cloneHead = root.next;
RandomListNode cur = root;
while (cur != null) {
RandomListNode cloneNode = cur.next;
cur.next = cur.next.next;
if (cloneNode.next != null) {
cloneNode.next = cloneNode.next.next;
}
cur = cur.next.next;
}
return cloneHead;
}
private void setRandomNode(RandomListNode newNode) {
RandomListNode cur = newNode;
while (cur != null) {
if (cur.random != null) {
cur.next.random = cur.random.next;
}
cur = cur.next.next;
}
}
private void copyNode(RandomListNode root) {
RandomListNode cur = root;
while (cur != null) {
RandomListNode insertNode = new RandomListNode(cur.label);
insertNode.next = cur.next;
cur.next = insertNode;
cur = cur.next;
}
}
}
class RandomListNode {
int label;
RandomListNode next = null;
RandomListNode random = null;
RandomListNode(int label) {
this.label = label;
}
}
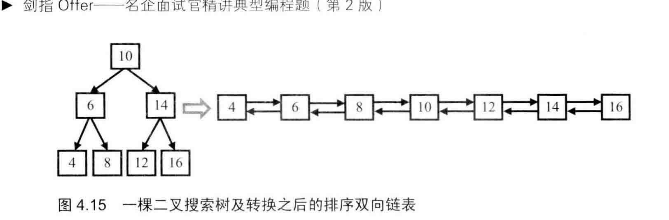
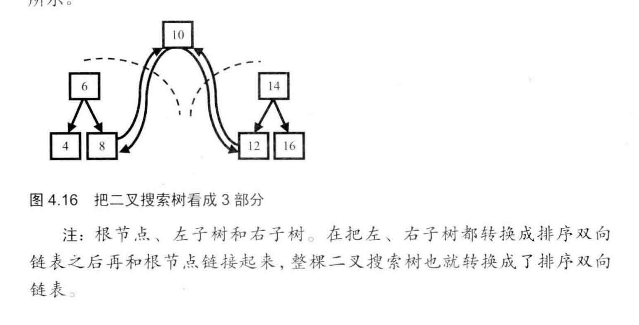
# 面试题36--二叉搜索树与双向链表(了解)
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
看到这道题我第一反映就是,二叉树的线索化,不过还是有些区别的,下面会讨论。按照二叉搜索树的特点,最左边的结点是值最小的,而题目要求得到排序的双向链表,所以基本确定下来中序遍历的方法。
/**
* 定义:转换后left表示pre,right表示next
* @param root 根结点
* @return
*/
public static BinaryTreeNode treeToLinkedList(BinaryTreeNode root) {
if(root==null) return root;
//链表尾节点
BinaryTreeNode lastNode=null;
//转换
lastNode=convert(root,lastNode);
//寻找返回的头结点
BinaryTreeNode head=lastNode;
while(head.left!=null) {
head = head.left;
}
return head;
}
/**
* 返回当前已转换好的链表的尾结点
* @param root 当前子树的根结点
* @param last 保存当前链表的最后一个指针
* @return 返回当前链表的最后一个结点
*/
public static BinaryTreeNode convert(BinaryTreeNode root,BinaryTreeNode last) {
if(root==null) return null;
BinaryTreeNode p=root;
//转换左子树
if(root.left!=null) last=convert(root.left,last);
//根结点的pre指向左子树的last,左子树的last的next指向根结点
p.left=last;
if(last!=null) last.right=p;
//last指向根结点
last=p;
//转换右子树
if(root.right!=null) last=convert(root.right,last);
return last;
}
# 面试题37--序列化二叉树
请实现两个函数,分别用来序列化和反序列化二叉树。

其实遇到空指针可以也用一个特殊的字符表示,比如“#”,这样前序遍历序列就可以表示唯一的一棵二叉树了。对于空指针也用一个字符表示,可称这样的序列为扩展序列。而二叉树的建立,必须先要建立根结点再建立左右子树(root为空怎么调用root.left是吧),所以必须前序建立二叉树,那么序列化时也应该用前序遍历,保证了根结点在序列前面。
不能使用中序遍历,因为中序扩展序列是一个无效的序列,比如
A B
/ \ \
B C 和 A 中序扩展序列都是 #B#A#C#
\
C
先来看序列化的代码,其实就是在前序遍历的基础上,如果遇到空指针就用“#”表示。
package com.lovedata.interview.N37_SerializeBinaryTrees;
import utils.TreeNode;
import utils.TreeOperation;
/**
* @author pengshuangbao
* @date 2021/2/24 9:11 AM
*/
public class SerializeBinaryTrees {
/**
* 序列化树
*
* @param root
* @return
*/
public String serialize(TreeNode root) {
if (root == null) {
return null;
}
// 使用一个sb来存储最后的数据
StringBuilder sb = new StringBuilder();
// 使用前序遍历
preOrder(root, sb);
return sb.toString();
}
private void preOrder(TreeNode root, StringBuilder sb) {
// 如果根节点是空,则需要返回一个#,占位
if (root == null) {
sb.append("# ");
return;
}
// 如果不为空,加上值
sb.append(root.val + " ");
preOrder(root.left, sb);
preOrder(root.right, sb);
}
/**
* 这里需要一个index,表示当前读到字符串的哪一个下标去了
*/
int index = -1;
public TreeNode deserialize(String sb) {
if (sb == null) {
return null;
}
String[] split = sb.split("\\s");
return reConstructTree(split);
}
private TreeNode reConstructTree(String[] split) {
// 没读取一个 index+1
++index;
// 获取当前index的值
String s = split[index];
if ("#".equals(s)) {
return null;
}
TreeNode treeNode = new TreeNode(Integer.valueOf(s));
treeNode.left = reConstructTree(split);
treeNode.right = reConstructTree(split);
return treeNode;
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(1);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(3);
TreeNode node4 = new TreeNode(4);
TreeNode node5 = new TreeNode(5);
TreeNode node6 = new TreeNode(6);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
node2.right = node5;
node2.left = node6;
TreeOperation.show(roo1);
String sb = new SerializeBinaryTrees().serialize(roo1);
System.out.println(sb);
TreeNode deserialize = new SerializeBinaryTrees().deserialize(sb);
TreeOperation.show(deserialize);
}
}
# 面试题38--字符串的排列
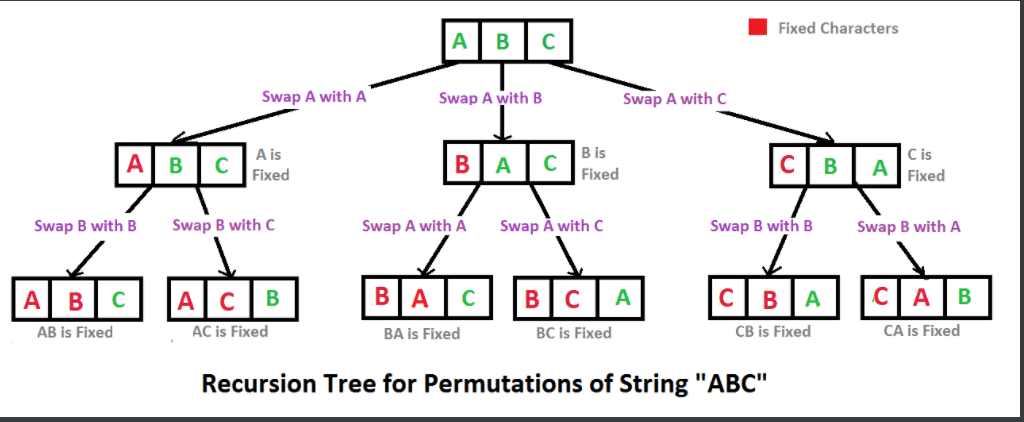
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
注意这道题求得是全排列。求若干字符组成的序列的所有排列可能,可以将字符序列分解成两部分:
- 第一个字符
- 第一个字符之后的字符序列
这样就把一个大问题分解成了小问题,然后对小问题继续采用相同的策略即可!
因为所有字符都可能处于第一个位置,我们可以把第一个字符和其后的所有字符交换位置,这样就保证了所有字符都会位于第一个字符处;交换后固定第一个字符,然后对于其后的字符序列,继续分成两部分:第一个字符和其后的字符序列......这是一个递归过程!
第一个字符和其后的所有字符依次交换位置可以用一个for循环完成,对于循环中的每一次交换:在交换位置后要对除第一个字符外的字符序列进行递归。**这里一定要注意,第一个字符首先要和自己交换一下。**一次递归调用结束后,需要将之前的交换复原,以保证下次交换依然是和第一个字符交换。比如abcd,第一个字符和第二个字符交换后变成bacd,此后固定b对acd递归,递归结束后,需要将bacd复原成abcd,以便下次a和c交换位置变成cbad......
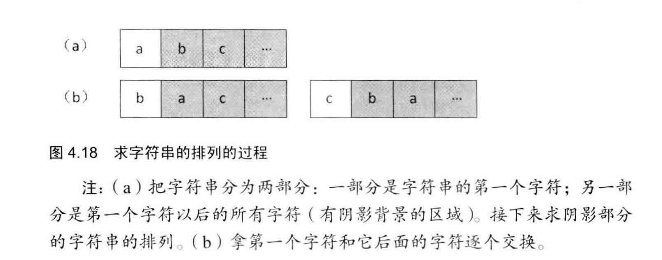
| Chars | Begin | List | i | 备注 |
|---|---|---|---|---|
| abc | 0 | [] | 第一次入栈 R0 | |
| abc | 0 | [] | 0 | swap |
| abc | 1 | [] | 第二次入栈R1 | |
| abc | 1 | [] | 1 | Begin为1循环 |
| abc | 1 | [] | 1 | Swap |
| abc | 2 | [] | 第三次入栈R2 | |
| abc | 2 | [abc] | Begin=len-1 存入abc,弹出R2 | |
| abc | 1 | [abc] | 1 | Swap |
| abc | 1 | [abc] | 2 | Begin为1循环 |
| acb | 1 | [abc] | 2 | Swap |
| acb | 2 | [abc] | 第四次入栈R3 | |
| acb | 2 | [abc,acb] | Begin=len-1 存入acb,弹出R3 | |
| abc | 1 | [abc,acb] | 2 | Swap |
| abc | 1 | [abc,acb] | 1 | 弹出R1 |
| abc | 1 | [abc,acb] | 1 | Swap |
| abc | 0 | [abc,acb] | 1 | |
| bac | 0 | [abc,acb] | 1 | Swap |
| bac | 1 | [abc,acb] | 第五次入栈R4 | |
| ... |
package com.lovedata.interview.N38_StringPermutation;
import java.util.ArrayList;
/**
* @author pengshuangbao
* @date 2021/2/24 10:55 AM
*
* 输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba
*/
public class StringPermutation {
public ArrayList<String> permutation(String str) {
ArrayList<String> list = new ArrayList<>();
if (str == null) {
return list;
}
char[] chars = str.toCharArray();
collect(chars, 0, list);
return list;
}
private void collect(char[] chars, int begin, ArrayList<String> list) {
if (begin == chars.length - 1) {
if (!list.contains(String.valueOf(chars))) {
list.add(String.valueOf(chars));
}
}
//从第一个字符串开始,持续往后
for (int i = begin; i < chars.length; i++) {
swap(chars, i, begin);
collect(chars, begin + 1, list);
swap(chars, i, begin);
}
}
private void swap(char[] chars, int i, int begin) {
char temp = chars[i];
chars[i] = chars[begin];
chars[begin] = temp;
}
public static void main(String[] args) {
System.out.println(new StringPermutation().permutation("abc"));
}
}
# 优化时间和空间效率
同一个算法,用循环和递归两种思路实现,时间效率大不一样。 递归本质是吧复杂问题分解成两个或者多个小的简单问题。 如果有重叠,则效率回非常差,虽然看起来简洁一些。
如果是顺序查找,需要O(n) ,如果是已经排好序的数组,则需要O(logn),如果事先构造好了Hash表,则需要O(1) 的时间查找。
# 面试题39--数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
可以先将数组排序,然后统计数字出现的次数,先将第一个数字出现次数初始化为1,如果遇到同样的数字,就加1,遇到不一样的就重新初始化为1重新开始计数,知道某个数字计数值大于n / 2(n是数组的长度),终止循环,返回当前数字就是我们要的答案。
# 切分法,时间复杂度O(n)
注**意到排序之后,如果数组中存在某个数字超过数组长度的一半,那么数组中间的数字必然就是那个出现次数超过一半的数字。**这就将问题转化成了求数组的中位数,快速排序使用的切分算法可以方便地找出中位数,且时间复杂度为O(n),找出中位数后还需要再遍历一边数组,检查该中位数是否出现次数超过数组长度的一半。总结一下,基于切分法有如下两个步骤:
- 切分法找出中位数
- 检查中位数
package com.lovedata.interview.N39_MoreThanHalfNumber;
/**
* @author pengshuangbao
* @date 2021/2/24 2:15 PM
* 数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
* 例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
*/
public class MoreThanHalfNumber {
public int moreThanHalfNumber(int[] array) {
if (array == null || array.length == 0) {
return 0;
}
int mid = select(array, array.length / 2);
return checkIsMoreThanHalfNumber(array, mid);
}
private int checkIsMoreThanHalfNumber(int[] array, int mid) {
int count = 0;
for (int i = 0; i < array.length; i++) {
if (array[i] == mid) {
count++;
}
}
return count > array.length / 2 ? mid : 0;
}
public int select(int[] array, int k) {
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = partition(array, low, high);
if (mid == k) {
return array[k];
} else if (mid < k) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return array[k];
}
/**
* 基于数组的特性
*
* @param array
* @return
*/
public int findNumMoreThanHalf(int[] array) {
if (array == null || array.length == 0) {
return 0;
}
int count = 1;
int result = array[0];
for (int i = 1; i < array.length; i++) {
if (count == 0) {
result = array[i];
count = 1;
} else if (array[i] == result) {
count++;
} else {
count--;
}
}
return checkIsMoreThanHalfNumber(array, result);
}
public int partition(int[] array, int low, int high) {
int x = array[low];
while (low < high) {
while (low < high && array[high] >= x) {
high--;
}
array[low] = array[high];
while (low < high && array[low] <= x) {
low++;
}
array[high] = array[low];
}
array[low] = x;
return low;
}
public static void main(String[] args) {
int[] array = {1, 2, 3, 2, 2, 2, 5, 4, 2};
System.out.println(new MoreThanHalfNumber().moreThanHalfNumber(array));
}
}
select方法是通用的选择排名为k的元素,只要参数传入n / 2即可求得中位数。partition方法会返回一个索引j,该索引的左半部分全小于索引出的值,右半部分全大于索引处的值,如果指定的排名k == j,那么问题就解决了;如果k < j,则需要在左半数组中继续查找;如果k > j,则需要在右半数组继续查找。循环中保证了low左边的值都小于arr[low, high],而high右边的值都大于arr[low, high],通过不断切分和k比较,直到子数组中只含有第k个元素,此时arr[0]~arr[k - 1]都小于a[k]而arr[k+1]即其后的所有都大于a[k],a[k]刚好是排名第k的元素。
另外while循环外还有一个return a[k],保证了当数组长度为1,即high == low时不能进入while循环,应该直接返回a[k].
找到中位数之后遍历一边数组,检查中位数出现次数是否超过数组长度一半即可。
# 面试题40--最小的k个数
输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
package com.lovedata.interview.N40_KLeastNumbers;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.PriorityQueue;
/**
* @author pengshuangbao
* @date 2021/2/24 2:47 PM
* 面试题40--最小的k个数
* > 输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
* ##
*/
@SuppressWarnings("Duplicates")
public class KLeastNumbers {
/**
* 使用快排的思想,需要改变数组的位置
* 切分法
*
* @param array
* @param k
* @return
*/
public ArrayList<Integer> getKLeastNumbers(int[] array, int k) {
ArrayList<Integer> arrayList = new ArrayList<>();
if (array == null || array.length == 0 || k > array.length || k <= 0) {
return arrayList;
}
select(array, k - 1);
for (int i = 0; i < k; i++) {
arrayList.add(array[i]);
}
return arrayList;
}
public int select(int[] array, int k) {
int low = 0;
int high = array.length - 1;
while (low <= high) {
int mid = partition(array, low, high);
if (mid == k) {
return array[k];
} else if (mid < k) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return array[k];
}
public int partition(int[] array, int low, int high) {
int x = array[low];
while (low < high) {
while (low < high && array[high] >= x) {
high--;
}
array[low] = array[high];
while (low < high && array[low] <= x) {
low++;
}
array[high] = array[low];
}
array[low] = x;
return low;
}
/**
* 上面两个方法都改变了输入数组
* 直接使用Java内置的优先队列
*/
public ArrayList<Integer> getLeastK(int[] input, int k) {
ArrayList<Integer> list = new ArrayList<>();
if (input == null || input.length == 0 || k > input.length || k == 0) {
return list;
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
for (int a : input) {
maxHeap.offer(a);
// 只要size大于k,不断剔除最大值,最后优先队列里只剩最小的k个
if (maxHeap.size() > k) {
maxHeap.poll();
}
}
list.addAll(maxHeap);
return list;
}
public static void main(String[] args) {
int[] array = {1, 2, 3, 2, 2, 2, 5, 4, 2};
System.out.println(new KLeastNumbers().getKLeastNumbers(array, 7));
System.out.println(new KLeastNumbers().getLeastK(array, 7));
}
}
# 面试题41--数据流中的中位数
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。

中位数将数组分成两部分,**中位数左边的部分比中位数右边的部分都要小,换言之:左边部分的最大值也不会超过右边部分的最小值。**要获取最大值、最小值,比较容易想到的就是最大堆和最小堆了。又注意到,被中位数分开的两个部分,其大小之差不会超过1。所以在往两个堆里存入元素时,要保证交替存入两个容器,比如:当前元素个数为奇数时,就默认存入最小堆中;当前元素个数为偶数时,就默认存入最大堆中;当前没有元素时,默认存入最大堆中。
为了保证中位数左边部分的最大值也不会超过右边部分的最小值,**应该使用最大堆存放较小元素,最小堆存放较大元素。**有两种特殊情况:
- 当前要存入最大堆中的元素比最小堆的最小值大,这样不能保证最大堆的最大值不会超过最小堆的最小值。此时需要将最小堆中的最小值弹出并存入最大堆中,并将当前元素存入最小堆中,其实就是将当前元素和最小堆的最小值交换了存储位置。
- 当前要存入最小堆的元素比最大堆的最大值小,这样也不能保证最大堆的最大值不会超过最小堆的最小值。此时需要将最大堆中的最大值弹出并存入最小堆中,并将当前元素存入最大堆中。
中位数的获取就很简单了,如果当前数据流中个数为奇数,则中位数一定是最大堆的最大值(因为上面规定了当前数据个数为偶数时存入最大堆中,之后数据个数变成奇数,因此要么最大堆的大小比最小堆一样,要么比最小堆大1);如果当前数据流中个数为偶数,那么要求平均数,这两个中间值一个是最大堆的最大值,一个是最小堆的最小值。
package com.lovedata.interview.N41_StreamMedian;
import java.util.Comparator;
import java.util.PriorityQueue;
/**
* @author pengshuangbao
* @date 2021/2/24 3:47 PM
*/
public class StreamMedian {
/**
* 最大堆,存中位数左边的数,也就是比中位数小的数,最大堆的最大值,肯定是比最小堆的最小值小
*/
private PriorityQueue<Integer> maxPQ = new PriorityQueue<Integer>(Comparator.reverseOrder());
/**
* 最小堆,村中位数右边的数,也就是比中位数大的数,最小堆的最小值,肯定比最大堆的最大值大
*/
private PriorityQueue<Integer> minPQ = new PriorityQueue<Integer>();
int count = 0;
public void insert(int number) {
//如果当前的count是0,则默认存入到最大堆,也就是左边的堆
if (count == 0) {
maxPQ.offer(number);
} else if ((count & 1) == 1) { // 如果当前总的数是奇数,则存入到最小堆
//又因为存入到最小堆的值比最大堆的最大值小,就不能保证右边的比左边的大了
//这个时候,就要把最大堆的最大值放到最小堆里面去,然后在把number存入到最大堆中去
if (number < maxPQ.peek()) {
minPQ.offer(maxPQ.poll());
maxPQ.offer(number);
} else {
minPQ.offer(number);
}
} else {
//如果是偶数,则存入到最大堆
//又因为存入到最大堆的值比最小堆的最小值大,就不能保证左边的比右边的小了
//这个时候,就要把最小堆的最小值放到最大堆里面去,然后在把number存入到最小堆中去
if (number > minPQ.peek()) {
maxPQ.offer(minPQ.poll());
minPQ.offer(number);
} else {
maxPQ.offer(number);
}
}
count++;
}
public Double getMedian() {
// 当数据流读个数为奇数时,最大堆的元素个数比最小堆多1,因此中位数在最大堆中
if ((count & 1) == 1) {
return Double.valueOf(maxPQ.peek());
}
// 当数据流个数为偶数时,最大堆和最小堆的元素个数一样,两个堆的元素都要用到
return Double.valueOf((maxPQ.peek() + minPQ.peek())) / 2;
}
public static void main(String[] args) {
StreamMedian s = new StreamMedian();
s.insert(1);
s.insert(2);
s.insert(3);
s.insert(3);
System.out.println(s.getMedian());
}
}
下面来比较下各个方法的效率。
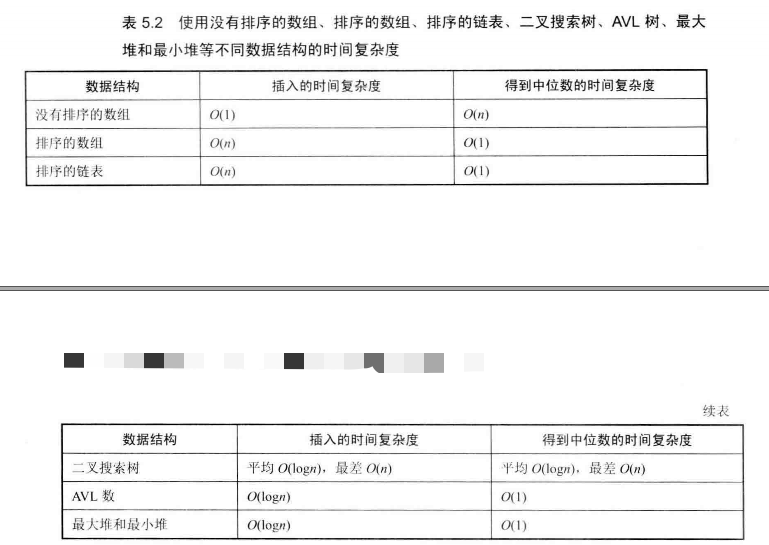
| 数据结构 | 插入复杂度 | 得到中位数的复杂度 |
|---|---|---|
| 没有排序的数组 | O(1) | O(n) |
| 有序数组 | O(n) | O(1) |
| 二叉查找树 | 平均O(lgn),最差O(n) | 平均O(lgn),最差O(n) |
| 最大堆、最小堆 | O(lg n) | O(1) |
# 面试题42--连续子数组的最大和
输入一个整型数组,数组里正负数都可能有,数组中的一个或者连续的多个整数组成一个子数组。求所有子数组的和的最大值,要求时间复杂度为O(n)
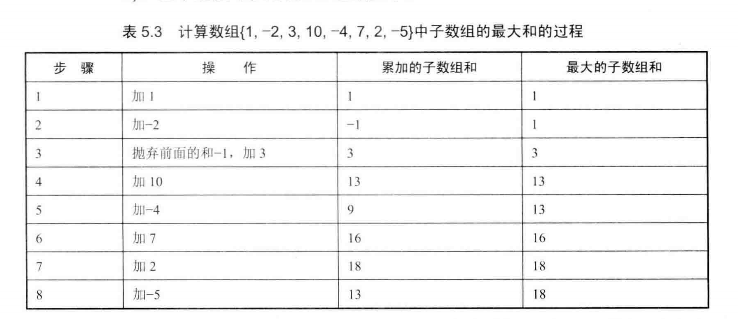
我们可以举例分析数组的特点比如{1, -2, 3, 10, -4, 7, 2, -5}。首先记录下第一个元素,先假设它为最大和。当1加上-2时变成了-1,再加上3等于2,3前面加了一堆还不如不加,所以应该直接从3开始加,即如果当前累加和是负数,那么它加上当前元素将使得新的累加和比当前元素还要小,此时应该将之前的累加和丢弃,从当前元素开始累加。
package com.lovedata.interview.N42_GreatestSumOfSubarrays;
/**
* @author pengshuangbao
* @date 2021/2/24 4:25 PM
* # 面试题42--连续子数组的最大和
* 输入一个整型数组,数组里正负数都可能有,数组中的一个或者连续的多个整数组成一个子数组。求所有子数组的和的最大值,要求时间复杂度为O(n)
*/
public class GreatestSumOfSubarrays {
public int greatestSumOfSubarrays(int[] array) {
if (array == null || array.length == 0) {
return 0;
}
//需要两个变量,当前和,也就是截止到当前值的和
int curSum = array[0];
//到目前为止得到的最大和,会和当前和做比较=
int maxSum = array[0];
for (int i = 1; i < array.length; i++) {
//如果当前和是个负数,那么也就是说,前面的和加上i-1就没什么用,加了等于没加,那么直接从当前值继续开始
if (curSum < 0) {
curSum = array[i];
} else {
curSum += array[i];
}
//如果后面在遇上了负数,这里就不会大于maxSum,则最大和并不会改变,直到再次加上正数才会改变
if (curSum > maxSum) {
maxSum = curSum;
}
}
return maxSum;
}
public static void main(String[] args) {
int[] array = {1, -2, 3, 10, -4, 7, 2, -5};
System.out.println(new GreatestSumOfSubarrays().greatestSumOfSubarrays(array));
}
}
# 面试题43--1~n整数中1出现的次数
输入一个整数n,求1~n这n个整数的十进制表示中1出现的次数,例如输入12, 1~12中出现1的有1、10、11、12共5次
# 计算每个数字出现1的次数
比较直接的思路就是写一个方法可以统计任意整数1的个数,然后用一个循环得到对1~n每一个数调用该方法统计总的1的出现次数。
package com.lovedata.interview.N43_NumberOf1;
/**
* @author pengshuangbao
* @date 2021/2/24 4:47 PM
*/
public class NumberOf1 {
public int getNumberOf2(int n) {
if (n < 0) {
n = Math.abs(n);
}
int sum = 0;
for (int i = 1; i <= n; i++) {
sum += numberOf1(i);
}
return sum;
}
private int numberOf1(int i) {
int count = 0;
while (i != 0) {
if (i % 10 == 1) {
count++;
}
i = i / 10;
}
return count;
}
public static void main(String[] args) {
System.out.println(new NumberOf1().getNumberOf2(12));
}
}
# 面试题45--把数组排成最小的数
输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组{3,32,321},则打印出这三个数字能排成的最小数字为321323。
这道题可以对数组排序,比如对于普通的数组{23, 12, 32},可能会想到按照自然序排序后,得到{12, 23, 32}然后直接拼接起来就得到了最小的数字122332,但是像题中的例子按照自然序排好后就是{3, 32, 321},如果直接拼接得到332321,是不是最小呢?可以发现排好后是{321, 32, 3},才能得到最小数321323。可见这已经不是自然序了,所以想到需要自定义一种比较方法,得到一种新的排序方式。
既然是要拼接数组中所有的数,保证拼接后的数最小,我们从最小的问题出发,当数组中只有两个数时,情况很简单,比如{3, 32},有用两种方式拼接他们"3"+"32"和"32"+"3",分别为332和323,因为323 < 332,所以将32排在3的前面,也就是对于数组中的任意两个数m和n,如何mn < nm,则应该将m排在n的前面。在Java中很好实现,只需重写一个Comparator即可。使用Java 8的lambda表达式可以简化这一过程。
package com.lovedata.interview.N45_SortArrayForMinNumber;
import java.util.ArrayList;
import java.util.ArrayList;
/**
* @author pengshuangbao
* @date 2021/2/24 7:39 PM
*/
public class SortArrayForMinNumber {
public String sortArrayForMinNumber(int[] array) {
if (array == null || array.length == 0) {
return null;
}
ArrayList<Integer> list = new ArrayList<Integer>();
for (int i = 0; i < array.length; i++) {
list.add(array[i]);
}
list.sort((a, b) -> (a + "" + b).compareTo(b + "" + a));
StringBuilder sb = new StringBuilder();
for (int i = 0; i < list.size(); i++) {
sb.append(list.get(i));
}
return sb.toString();
}
public static void main(String[] args) {
int[] array = {23, 12, 32};
int[] array1 = {3, 32, 321};
System.out.println(new SortArrayForMinNumber().sortArrayForMinNumber(array));
System.out.println(new SortArrayForMinNumber().sortArrayForMinNumber(array1));
}
}
# 面试题47--礼物的最大价值
在一个mxn的棋盘的每一格斗放油一个礼物,每个礼物都有一定的价值(大于0)从棋盘的左上角开始,每次可以往右边或者下边移动一格,知道到达棋盘的右下角。给定一个棋盘和上面的礼物,计算我们最多可以拿到多少价值的礼物

package com.lovedata.interview.N47_MaxValueOfGifts;
/**
* @author pengshuangbao
* @date 2021/2/25 3:26 PM
* # 面试题47--礼物的最大价值
* > 在一个mxn的棋盘的每一格斗放油一个礼物,每个礼物都有一定的价值(大于0)从棋盘的左上角开始,每次可以往右边或者下边移动一格,
* 知道到达棋盘的右下角。给定一个棋盘和上面的礼物,计算我们最多可以拿到多少价值的礼物
* ## 递归--两个方向的深度优先搜索
*/
public class MaxValueOfGifts {
/**
* 通过递归的方式
* 有很多重复的计算。
*递归--两个方向的深度优先搜索
* @param gift
* @param rows
* @param cols
* @return
*/
public int getMax(int[] gift, int rows, int cols) {
if (gift == null || gift.length == 0) {
return 0;
}
int[] max = new int[1];
select(gift, rows, cols, 0, 0, 0, max);
return max[0];
}
private void select(int[] gift, int rows, int cols, int row, int col, int curVal, int[] max) {
if (row >= rows || col >= cols) {
return;
}
int cur = gift[row * cols + col];
curVal += cur;
if (curVal > max[0]) {
max[0] = curVal;
}
select(gift, rows, cols, row + 1, col, curVal, max);
select(gift, rows, cols, row, col + 1, curVal, max);
}
/**
* 通过动态规划获取
* * 方法2:动态规划,到达f(i,j)处拥有的礼物价值和有两种情况:
* * 1、从左边来,即f(i, j) = f(i, j -1) + gift(i, j)
* * 2、从上边来,即f(i, j) = f(i -1, j) + gift(i, j)
* *
* * 保证到达每一个格子得到的礼物价值之和都是最大的,也就是取max[f(i, j-1), f(i-1, j)] +gift(i, j)
* * 可以发现,要知道当前格子能获得最大礼物价值,需要用到当前格子左边一个和上面一个格子的最大礼物价值和
*
* @param gift
* @param rows
* @param cols
* @return
*/
public int getMaxVal(int[] gift, int rows, int cols) {
if (gift == null || gift.length == 0) {
return 0;
}
int[][] maxVal = new int[rows][cols];
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
int up = 0;
int left = 0;
//如果row大于0,则肯定不是第一行
if (row > 0) {
up = maxVal[row - 1][col];
}
//如果col>与0,则肯定不是第一列
if (col > 0) {
left = maxVal[row][col - 1];
}
maxVal[row][col] = Math.max(up, left) + gift[row * cols + col];
}
}
return maxVal[rows - 1][cols - 1];
}
/**
* 当前礼物的最大价值只依赖$f(i-1, j)$和$f(i, j -1)$这两个格子,因此只需要当前行i,
* 第j列的前面几个格子,也就是$f(i, 0)$~$f(i, j-1)$;以及i -1行的,第j列及其之后的几个格子,也就是$f(i-1, j)$~$f(i-1, cols-1)$
* 两部分加起来的个数刚好是棋盘的列数cols。所以只需要一个长度为cols的一维数组即可,优化如下。
*
* @param gift
* @param rows
* @param cols
* @return
*/
public int betterGetMaxVal(int[] gift, int rows, int cols) {
if (gift == null || gift.length == 0) {
return 0;
}
int[] maxVal = new int[cols];
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
int up = 0;
int left = 0;
if (row > 0) {
up = maxVal[col];
}
if (col > 0) {
left = maxVal[col - 1];
}
maxVal[col] = Math.max(up, left) + gift[row * cols + col];
}
}
return maxVal[cols - 1];
}
public static void main(String[] args) {
int[] gift = {1, 10, 3, 8, 12, 2, 9, 6, 5, 7, 4, 11, 3, 7, 16, 5};
System.out.println(new MaxValueOfGifts().getMax(gift, 4, 4));
System.out.println(new MaxValueOfGifts().getMaxVal(gift, 4, 4));
System.out.println(new MaxValueOfGifts().betterGetMaxVal(gift, 4, 4));
}
}
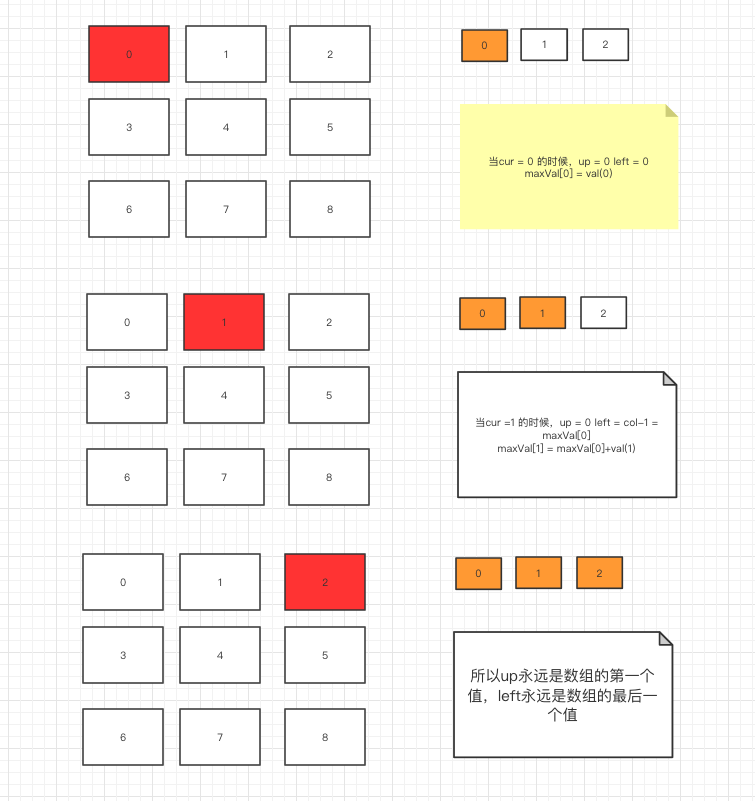
# 面试题48--最长不含重复字符串的子字符串
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。假设字符串中只包含'a'~'z'之间的字符,例如在字符串"arabcacfr"中,最长的不含重复字符的子字符串是"acfr",长度为4
动态规划,定义$f(i)$表示以第i个字符为结尾的不含重复字符的子字符串长度。
如果第i个字符之前没有出现过,则$f(i) = f(i -1) +1$,比如‘abc',$f(0) = 1$是必然的,然后字符’b‘之前没有出现过,则$f(1) = f(0)+1$, 字符’c'之前没有出现过,那么$f(2) = f(1) +1$,每次计算都会用到上一次计算的结果。
如果第i个字符之前出现过呢?找到该字符上次出现的位置preIndex,当前位置i - preIndex就得到这两个重复字符之间的距离,设为d。此时有两种情况
如果
d <= f(i-1),说明当前重复字符必然在f(i-1)所对应的字符串中,比如’bdcefgc‘,当前字符c前面出现过了,preIndex为2,此时d = 6 -2 = 4,小于f(i -1) = 7 (bdcefg)我们只好丢弃前一次出现的字符c及其前面的所有字符,得到当前最长不含重复字符的子字符串为’efgc‘,即f(i) = 4, 多举几个例子就知道,应该让f(i) = d;如果
d > f(i-1), 这说明当前重复字符必然在f(i-1)所对应的字符串之前,比如erabcdabr当前字符r和索引1处的r重复,preIndex =1, i = 8,d = 7。而f(i -1) = 4 (cdab),此时直接加1即可,即f(i) = f(i-1) +1
package com.lovedata.interview.N48_LongestSubstringWithoutDup;
/**
* @author pengshuangbao
* @date 2021/2/25 4:45 PM
*/
public class LongestSubstringWithoutDup {
public int getLongestSubstringWithoutDup(String str) {
if (str == null || str.length() == 0) {
return 0;
}
int curLen = 0;
int maxLen = 0;
int[] position = new int[26];
for (int i = 0; i < 26; i++) {
position[i] = -1;
}
for (int i = 0; i < str.length(); i++) {
int cur = str.charAt(i);
int preIndex = position[cur - 'a'];
//两种情况
// 第一种情况 当前字符串从未出现过,则长度加1
// 第二种情况 当 当前字符串到上一次出现的长度大于当前的最大长度,比如 adcda, d的最大长度为2,而a到第一个a的是 5 ,而长度大于2,说明a出现在 cd之前,不重复,则
// 长度为 2+1
if (preIndex == -1 || (i - preIndex > curLen)) {
curLen++;
} else {
// 这种情况,到上一个出现的距离小于 curLen,则表示重复了,需要重新计算
// 重新计算之前了,因为要求最大的,所以,后面的不一定就比前面的大,所以要把这个值暂存一下,后面可能用的到
if (curLen > maxLen) {
maxLen = curLen;
}
curLen = i - preIndex;
}
//然后还要在存一下当前字符出现的坐标
position[cur - 'a'] = i;
}
if (curLen > maxLen) {
maxLen = curLen;
}
return maxLen;
}
public static void main(String[] args) {
System.out.println(new LongestSubstringWithoutDup().getLongestSubstringWithoutDup("arabcacrfe"));
}
}
# 时间效率与空间效率的平衡
硬件一直在摩尔定律发展,内存一年翻番。
内存增加迅速,允许牺牲一定的空间为代价换取时间性能,以尽可能缩短软件相应时间
很多时候时间效率和空间效率就像鱼与熊掌不可兼得。
# 面试题49--丑数
把只包含因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含因子7。习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
res[0] = 1
| i | res | t2 | t3 | t5 |
|---|---|---|---|---|
| 1 | [1,2] | 1 | 0 | 0 |
| 2 | [1,2,3] | 1 | 1 | 0 |
| 3 | [1,2,3,4] | 2 | 1 | 0 |
| 4 | [1,2,3,4,5] | 2 | 1 | 1 |
| 5 | [1,2,3,4,5,6] | 3 | 2 | 1 |
| 6 | [1,2,3,4,5,6,8] | 4 | 2 | 1 |
| 7 | [1,2,3,4,5,6,8,9] | 4 | 3 | 1 |
| 8 | [1,2,3,4,5,6,8,9,10] | 5 | 3 | 2 |
| 9 | [1,2,3,4,5,6,8,9,10,12] | 6 | 4 | 2 |
// 比如 i =1 的时候,三个分别乘以最小数为2 下个丑数是2,那么当前集合为{1,2},刚才的2 是1x2得到的,因此下一个和2相乘的,肯定不可能是 1了,你得大于2啊,所以肯定是2(因为丑数已经有序了),直接选择下一个就可以了,选择又得到了 4 3 5 得到最小的是3,所以为 {1,2,3},,刚才3由 1x3得到,所以下一个和3相乘的。应该是 下一个 2,然后又得到了 4 6 4 ,所以应该是 4 不断重复
package com.lovedata.interview.N49_UglyNumber;
/**
* 把只包含因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含因子7。习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
*/
public class UglyNumber {
/**
* 1 2 3 4 5 6 8 9 10 12
* <p>
* 丑数应该是另一个丑数 乘以 2,3,4得到的结果(1除外)
* 创建一个数组,里面都是排好序的丑数, 每个都是前面的丑数乘以 2 3 5 得到的
* 关键:怎么确保丑数是排好序的
* 假设有多个排好序的丑数,最大的为M
* 如何产生下一个丑数,该数肯定是前面某个丑数乘以 2 3 5
* 比较笨的,把前面每个乘以2,拿出第一个大于M的M2,并且同理拿到M3 M5,只需取最小的就是下一个丑数了。
* <p>
* 把每个数分别 乘以 2 3 5 是可以 但是不是必须的。
* 因为丑数是顺序存放在数组中,对于乘以2而言,肯定有T2,在他之前的每个丑数乘以2得到的都会小于已有最大臭鼠
* 在他之后的结果都会太大,我们只需几下t2,, 3 5 同理
*
* @param index
* @return
*/
public int uglyNumber(int index) {
if (index <= 0) {
return 0;
}
int t2 = 0;
int t3 = 0;
int t5 = 0;
int[] res = new int[index];
// 第一个丑数为1
res[0] = 1;
for (int i = 1; i < index; i++) {
// // 比如 i =1 的时候,三个分别乘以最小数为2 下个丑数是2,那么当前集合为{1,2},刚才的2 是1x2得到的
// ,因此下一个和2相乘的,肯定不可能是 1了,你得大于2啊,所以肯定是2(因为丑数已经有序了),
// 直接选择下一个就可以了,选择又得到了 4 3 5 得到最小的是3,所以为 {1,2,3},,刚才3由 1x3得到,
// 所以下一个和3相乘的。应该是 下一个 2,然后又得到了 4 6 4 ,所以应该是 4 不断重复
int m2 = res[t2] * 2;
int m3 = res[t3] * 3;
int m5 = res[t5] * 5;
// 三个候选中最小的就是下一个丑数
res[i] = Math.min(m2, Math.min(m3, m5));
// 选择某个丑数后ti * i,指针右移从丑数集合中选择下一个丑数和i相乘,
// 注意是三个连续的if,也就是三个if都有可能执行。这种情况发生在三个候选中有多个最小值,指针都要右移,不然会存入重复的丑数
if (res[i] == m2) {
t2++;
}
if (res[i] == m3) {
t3++;
}
if (res[i] == m5) {
t5++;
}
}
return res[index - 1];
}
public static void main(String[] args) {
System.out.println(new UglyNumber().uglyNumber(10));
}
}
# 面试题50--第一个只出现一次的字符
找出字符串中找出第一个只出现一次的字符,比如输入“abacceff",则输出'b'
要想知道某个字符是不是只出现了一次,必须遍历字符串的每个字符。**因此可以先遍历一次,统计每个字符出现次数。再遍历一次,遇到某个字符出现字符为1就立即返回。**统计每个字符出现次数,可以用哈希表,不过如果输入中都是ASCII码,那么使用0-255表示即可。这样使用一个int[] count = new int[256]就能代替哈希表了,以count[someChar] = times这种方式表示某个字符出现的次数。比如‘a’的ASCII码是97,那么count[97]就表示了字符'a'的出现次数,以此类推。
package Chap5;
public class FirstAppearOnceChar {
/**
* 返回第一个不重复字符
*/
public char firstNotRepeatingChar(String str) {
if (str == null || str.length() == 0) return '\0';
int[] count = new int[256];
for (int i = 0; i < str.length(); i++) {
count[str.charAt(i)]++;
}
for (int i = 0; i < str.length(); i++) {
if (count[str.charAt(i)] == 1) return str.charAt(i);
}
return '\0';
}
/**
* 返回第一个不重复字符在字符串中的索引
*/
public int firstAppearOnceChar(String str) {
if (str == null || str.length() == 0) return -1;
int[] count = new int[256];
for (int i = 0; i < str.length(); i++) {
count[str.charAt(i)]++;
}
for (int i = 0; i < str.length(); i++) {
if (count[str.charAt(i)] == 1) return i;
}
return -1;
}
}
上面两个方法,一个是返回第一个只出现一次的字符,一个返回第一个只出现一个的字符的索引,思路都一样。根据count[someChar]获取某个字符的出现次数时间复杂度为O(1),对于长度为n的字符串,总的复杂度为O(n).
不过如果输入中含有特殊符号或者中文等,256位的ASCII表就不够用了,需要上Unicode了,总之看题目要求吧,要想通用就哈希表。
# 相关题目
# 扩展一
定义一个函数,输入两个字符串,从第一个字符串中删除在第二个字符串中出现过的所有字符。比如第一个字符串"google",第二个字符串为"aeiou",删除后得到"ggl".
使用一个boolean occur[] = new int[256]布尔型数组,对于第二个字符串中的每个字符,标记为true表示出现过。遍历第一个字符串,判断每个字符在occur中是不是fale,为false说明该字符没有在第二个字符串中出现过,保留。
/**
* 从第一个字符串中删除第二个字符串中出现过的所有字符
*/
public String deleteFromAnother(String str, String another) {
if (str == null || str.length() == 0 || another == null || another.length() == 0) return str;
boolean[] occur = new boolean[256];
StringBuilder sb = new StringBuilder();
for (int i = 0; i < another.length(); i++) {
occur[another.charAt(i)] = true;
}
for (int i = 0; i < str.length(); i++) {
if (!occur[str.charAt(i)]) sb.append(str.charAt(i));
}
return sb.toString();
}
# 扩展二
定义一个函数,删除一个字符串中所有重复出现的字符,比如输入"google"返回"gole"
使用一个boolean occur[] = new int[256]布尔型数组,记录某个字符是否出现过。刚开始都初始化false,每添加一个字符就标记为true,这样下次遇到重复字符就不会再添加了。
/**
* 删除字符串中所有的重复字符
*/
public String deleteRepeating(String str) {
if (str == null || str.length() == 0) return str;
boolean[] occur = new boolean[256];
StringBuilder sb = new StringBuilder();
for (int i = 0; i < str.length(); i++) {
char ch = str.charAt(i);
if (!occur[ch]) sb.append(ch);
occur[ch] = true;
}
return sb.toString();
}
# 扩展三
变位词,如果两个单词含有相同的字母且每个字母出现的次数还一样,那么这两个单词互为变位词。定义一个函数判断两个字符串是不是互为变位词。
两个字符串含有相同的字母、每个字母出现的次数一样,先统计第一个字符串每个字符出现的次数,然后遍历第二个字符串,对于每个出现的字符,将统计表中相应字符的出现次数减1,如果啷个字符串是变位词,那么遍历结束后,统计表中每个字符出现的字符都是0。
/**
* 变位词
*/
public boolean hasSameChar(String s1, String s2) {
if (s1 == null || s2 ==null) return false;
int[] count = new int[256];
// 统计第一个字符串
for (int i = 0; i < s1.length(); i++) {
count[s1.charAt(i)]++;
}
// 第二个字符串中如果有该字符,就减去
for (int i = 0; i < s2.length(); i++) {
count[s2.charAt(i)]--;
}
// 如果是变位词,最后count数组每个位置都是0
for (int i = 0; i < 256; i++) {
if (count[i] != 0) return false;
}
return true;
}
# 题目二
字符流中第一个只出现一次的字符。 这次字符串是动态变化的了,比如现在只从字符流中读取了两个字符为"go"那么字符流中第一个只出现一次的字符是'g',等到从字符流中读取了前6个字符"google"时,第一个只出现一次的字符变成了'l'.
使用一个insert函数模拟从字符流中读到一个字符。这次统计表int[] occur = new int[256]记录的是字符出现的索引.
- 如果某个字符出现过,那么
occur[someChar] >= 0; - 对于没有出现过的字符,令
occur[someChar] = -1; - 如果某个字符第二次出现,令
occur[someChar] = -2。
要获得当前字符串中第一个只出现一次的,只需从所有occur[someChar] >= 0中结果中找出出现索引最小的那个字符即可。
package Chap5;
public class AppearOnceInStream {
// 记录某个字符出现的索引
private int[] count;
// 当前读取到的字符在字符串中的索引
private int index;
public AppearOnceInStream() {
count = new int[256];
for (int i = 0; i < count.length; i++) {
count[i] = -1;
}
}
// 模拟读取字符流中的下一个字符
public void insert(char c) {
if (count[c] == -1) count[c] = index;
else if (count[c] >= 0) count[c] = -2;
index++;
}
public char firstAppearOnceChar() {
int minIndex = Integer.MAX_VALUE;
char c = '\0';
for (int i = 0; i < count.length; i++) {
// 从所有count[i] >= 0的结果中找出最小的索引就是第一个只出现一次的字符
if (count[i] >= 0 && count[i] < minIndex) {
minIndex = count[i];
c = (char)i;
}
}
return c;
}
public static void main(String[] args) {
AppearOnceInStream a = new AppearOnceInStream();
a.insert('g');
a.insert('o');
System.out.println(a.firstAppearOnceChar());
a.insert('o');
a.insert('g');
a.insert('l');
a.insert('e');
System.out.println(a.firstAppearOnceChar());
}
}
# 面试题 52--两个链表的第一个公共结点
输入两个单链表,找出它们的第一个公共结点。
这道题有一个隐含条件:单链表只有一个next指针,如果两个链表有公共结点,那么从第一个公共结点前的一个结点开始,两个链表的next都指向同一个结点了。通俗点说就是两条路汇聚成了一条。
# 两个链表,逆序比较
比如一条链表{1, 5, 6, 7, 8}另外一条{2, 3, 4, 5, 6, 7, 8}从结点5开始后面的结点都完全一样了。既然后面的结点完全一样,我们可以从后往前比较两个链表当遇到某两个结点不同时,上次比较的结点就是逆序的最后一个公共结点了,即正序的第一个公共结点。
为了可以从后往前比较两个结点,栈可以实现我们的想法。
package com.lovedata.interview.N52_FirstCommonNodesInLists;
import utils.ListNode;
import java.util.LinkedList;
/**
* @author pengshuangbao
* @date 2021/3/2 3:41 PM
*/
public class FirstCommonNodesInLists {
/**
* 方法1:两个辅助栈,从尾到头,找到最后一个相同的结点
*/
public ListNode findFirstCommonNodeStack(ListNode pHead1, ListNode pHead2) {
ListNode cur1 = pHead1;
ListNode cur2 = pHead2;
LinkedList<ListNode> stack1 = new LinkedList<>();
LinkedList<ListNode> stack2 = new LinkedList<>();
// 分别存入两个栈中
while (cur1 != null) {
stack1.push(cur1);
cur1 = cur1.next;
}
while (cur2 != null) {
stack2.push(cur2);
cur2 = cur2.next;
}
// 用于记录逆序的上一个公共结点
ListNode publicNode = null;
while (!stack1.isEmpty() && !stack2.isEmpty()) {
if (stack1.peek() == stack2.pop()) {
publicNode = stack1.pop();
}
// 当前比较的不相同时,返回逆序的最后一个公共结点(也就是正序的第一个公共结点)
else {
return publicNode;
}
}
return publicNode;
}
}
# 面试中的各项能力



# 沟通能力和学习能力
系统越来越复杂,团队越来越大,开发、测试、经历 沟通交流越来越重要。
介绍项目经验、介绍解题思路的时候都需要 逻辑清晰明了,语言详略得当、表述的时候终点突出,观点明确。
知之为知之,不知为不知。千万不能不懂装懂。 也就是说不要把自己不熟悉的领域写成熟悉,面试官一问便知。
# 学习能力
计算机是一门更新速度快的学科,每年都有新技术涌现。
软件工程师需要具备很强的学习能力。
只有具备很强的学习能力和学习愿望的人,才能不断完善自己的知识结构,不断学习新的先进技术,让自己的职业生涯保持长久的生命力。
# 两种方法考验学习能力:
- 最近在看什么书或者在做什么项目,从中学到了哪些新技术。考察学习愿望和学习能力。
- 抛出一个新概念, 能不能在较短时间内理解这个新概念并且解决
# 善于学习、沟通的人也善于提问
面试官有一个重要的任务,就是考差学习愿望和学习能力。
面试官提出一个新概念,没听说过,于是在已有的理解上提出进一步的问题,在得到回复后,几个来回,掌握了这个概念。体现了学习能力

# 知识迁移能力
所谓学习能力,很重要的一点: 根据已经掌握的知识,技术能够迅速学习理解新的技术并且运用到实际工作中去。 也就是知识迁移能力。
考验迁移能力的一种方法是把经典的问题,稍作变换,期待应聘者能找到和经典问题的联系,从中收到启发,把解决问题的思路迁移过来解决新的问题。
另一种方法,先问一个简单的问题,在解答完成之后,再追问一个相关的同时难度更大的问题。
通俗的说法就是“举一反三”
# 面试题51--在排序数组中查找数字
# 面试题1
统计一个数字在排序数组中出现的次数。
package com.lovedata.interview.N53_01_NumberOfK;
/**
* @author pengshuangbao
* 统计一个数字在排序数组中出现的次数。
* @date 2021/3/4 5:41 PM
*/
public class NumberOfK {
/**
* 常见方法 O(N)
*
* @param array
* @return
*/
public int numberOfK1(int[] array, int k) {
if (array == null || array.length == 0) {
return -1;
}
int count = 0;
for (int i = 0; i < array.length; i++) {
if (array[i] == k) {
count++;
}
}
return count;
}
/**
* 使用二分查找方法,先找到第一个,在找到第二个,因此时间复杂度还是 O(logn)
* O(logn)
*
* @param array
* @param k
* @return
*/
public int numberOfK2(int[] array, int k) {
if (array == null || array.length == 0) {
return -1;
}
//先找第一个出现的下标
int first = getFirstK(array, k, 0, array.length - 1);
//找最后一个出现的下标
int last = getLastK(array, k, 0, array.length - 1);
if (last == -1 && first == -1) {
return -1;
} else {
return last - first + 1;
}
}
private int getLastK(int[] array, int k, int low, int high) {
while (low <= high) {
int mid = low + (high - low) / 2;
if (k < array[mid]) {
high = mid - 1;
} else if (k > array[mid]) {
low = mid + 1;
} else {
// mid 要小于最大坐标,并且 mid的下一个也是k,说明还不是最后一个,继续往后找
if (mid < array.length - 1 && array[mid + 1] == k) {
low = mid + 1;
} else {
return mid;
}
}
}
return -1;
}
private int getFirstK(int[] array, int k, int low, int high) {
while (low <= high) {
int mid = low + (high - low) / 2;
if (k < array[mid]) {
high = mid - 1;
} else if (k > array[mid]) {
low = mid + 1;
} else {
// 如果mid == k 并且 mid 要大于0,并且他的前一个也是k,说明不是第一个,则继续在前面找
if (mid > 0 && array[mid - 1] == k) {
high = mid - 1;
} else {
// 否则的花,当前这个就是第一个
return mid;
}
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = {1, 2, 3, 3, 3, 3, 4};
System.out.println(new NumberOfK().numberOfK1(arr, 3));
System.out.println(new NumberOfK().numberOfK2(arr, 3));
}
}
# 题目2
0~n-1中缺失的数 一个长度为n -1的递增排序数组中的所有数字都是唯一的,并且每个数字的都在范围0~n-1之内。在范围内0~n-1内的n个数字中有且只有一个数字不在该数组中,找出这个数字
package com.lovedata.interview.N53_02_MissingNumber;
/**
* @author pengshuangbao
* 0~n-1中缺失的数
* 一个长度为n -1的递增排序数组中的所有数字都是唯一的,并且每个数字的都在范围0~n-1之内。在范围内0~n-1内的n个数字中有且只有一个数字不在该数组中,找出这个数字
* @date 2021/3/4 7:34 PM
*/
public class MissingNumber {
public int findMissing(int[] arr) {
if (arr == null || arr.length == 0) {
return -1;
}
int low = 0;
int high = arr.length - 1;
int len = arr.length;
while (low <= high) {
int mid = low + (high - low) / 2;
if (arr[mid] != mid) {
if (mid == 0 || arr[mid - 1] == mid - 1) {
return mid;
} else {
high = mid - 1;
}
} else {
low = mid + 1;
}
}
if (low == len) {
return len;
}
return -1;
}
public static void main(String[] args) {
int[] arr = {0, 1, 2, 3, 4};
int[] arr1 = {0, 1, 2, 4};
System.out.println(new MissingNumber().findMissing(arr));
System.out.println(new MissingNumber().findMissing(arr1));
}
}
# 题目3
数组中数值和下标相等的元素。 假设一个单调递增的数组里的每个元素都是整数并且是唯一的。找出数组中任意一个数值等于其下标的元素。比如在数组{-3, -1, 1, 3, 5},数字3和它的下标相等
package com.lovedata.interview.N53_03_IntegerIdenticalToIndex;
/**
* @author pengshuangbao
* @date 2021/3/4 7:54 PM
* 数组中数值和下标相等的元素。
* 假设一个单调递增的数组里的每个元素都是整数并且是唯一的。找出数组中任意一个数值等于其下标的元素。比如在数组{-3, -1, 1, 3, 5},数字3和它的下标相等
*/
public class IntegerIdenticalToIndex {
public int findIntegerIdenticalToIndex(int[] arr) {
if (arr == null || arr.length == 0) {
return -1;
}
int low = 0;
int high = arr.length - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if (arr[mid] == mid) {
return mid;
} else if (arr[mid] > mid) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = {-3, -1, 1, 3, 5};
System.out.println(new IntegerIdenticalToIndex().findIntegerIdenticalToIndex(arr));
}
}
# 面试题54--二叉搜索树中排名为k的结点
给定一颗二叉搜索树,请找出排名第k的结点。

注意是二叉搜索树,这说明对于任何结点,有父结点大于其左子结点且小于右子结点。如果中序遍历这棵树,就能得到递增排序的序列。
接下来就很简单了,只需中序遍历到第k个结点,然后立即返回就行了。感觉对于这道题,非递归的中序遍历更好写一点。
package com.lovedata.interview.N54_KthNodeInBST;
import java.util.LinkedList;
import utils.TreeNode;
import utils.TreeOperation;
/**
* @author pengshuangbao
* @date 2021/3/4 8:13 PM
*/
public class KthNodeInBST {
public TreeNode findKthNode(TreeNode root, int k) {
if (root == null || k <= 0) {
return null;
}
int count = 0;
LinkedList<TreeNode> stack = new LinkedList<TreeNode>();
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
if (!stack.isEmpty()) {
root = stack.pop();
if (++count == k) {
return root;
}
root = root.right;
}
}
return null;
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(3);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(4);
TreeNode node4 = new TreeNode(1);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
TreeOperation.show(roo1);
System.out.println("---");
System.out.println(new KthNodeInBST().findKthNode(roo1, 2));
System.out.println(new KthNodeInBST().findKthNode(roo1, 6));
}
}
# 面试题55-二叉树的深度
# 题目一
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
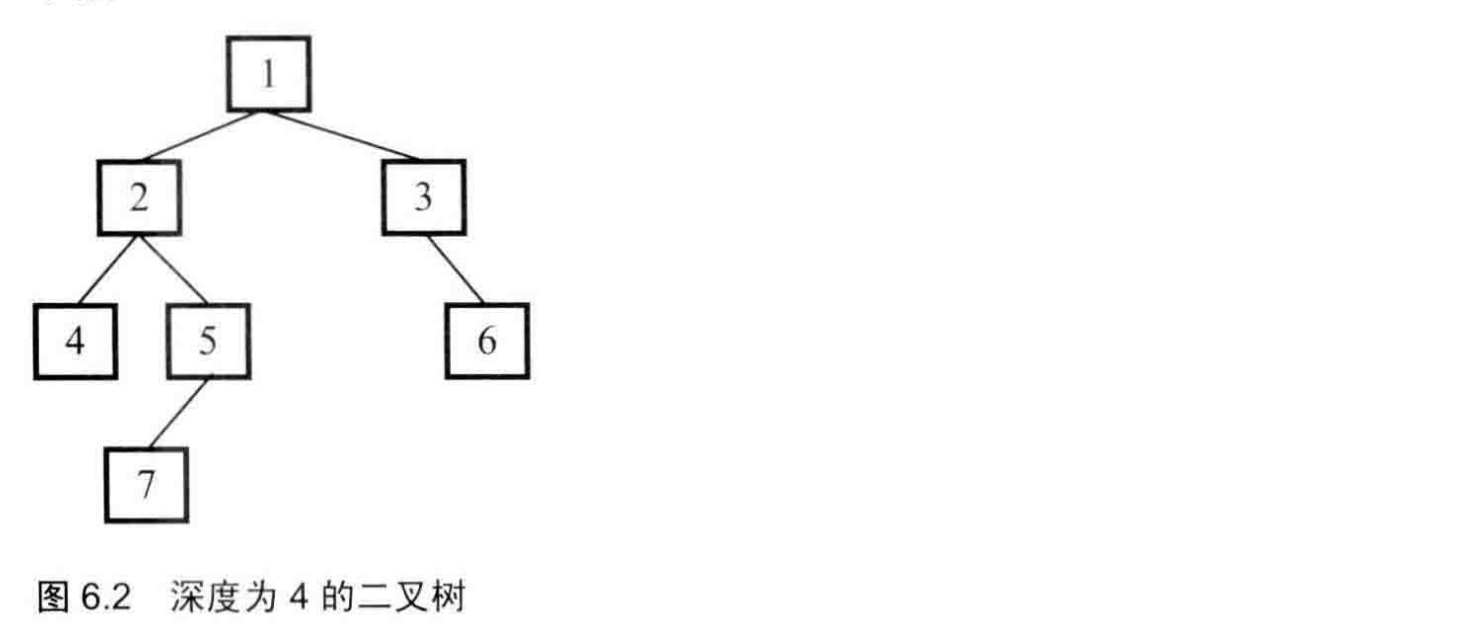
# 递归版本
很容易想到使用递归,根结点处的深度为1,既然要求树的最长路径,必然从根结点的左右子树中选出深度更大的那棵子树,也就是整棵树的深度为
$$depth(root) = max[depth(root.left), depth(root.right)] + 1$$
加1是因为要加上树的根结点。那么对于每棵子树,也要按照这样的规则——挑选出深度更大的子树并加上1,也就得到了以当前结点为根结点的二叉树的深度。这是个递归结构。
# 非递归版本
求深度,其实就是求这棵二叉树有多少层。于是采用BFS的层序遍历。关键就是怎么知道什么时候处理完了二叉树的一层?我们来模拟一下:
就假设这是棵满二叉树吧,根结点先入队列,此时队列中结点个数为1,接着会弹出这唯一的根结点,同时入列两个结点,此时第一层处理完毕;
现在队列中结点个数为2,我们出列两次,4个结点又会入列,此时第二层处理完毕;
现在队列中结点个数为4,我们出列4次,8个结点又会入列,此时第三层处理完毕....
发现规律了吗?**每次要出列前,先得到队列中现有的结点个数,假设是m,那么就在循环内出列m次,随即跳出循环,这样就算处理完一行了。**跳出循环后只需要将深度自增,最后层序遍历完毕也就得到了二叉树的深度。
package com.lovedata.interview.N55_01_TreeDepth;
import utils.TreeNode;
import utils.TreeOperation;
import java.util.LinkedList;
import java.util.Queue;
/**
* @author pengshuangbao
* @date 2021/3/5 9:59 AM
* 输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
*/
public class TreeDepth {
/**
* 很容易想到使用递归,出口就是根位null的时候就是0
* 然后求左边节点的深度和右边节点的深读
* 根节点就是等于两者最大的+1;
*
* @param root
* @return
*/
public int getDepth(TreeNode root) {
if (root == null) {
return 0;
}
int left = getDepth(root.left);
int right = getDepth(root.right);
return left > right ? left + 1 : right + 1;
}
/**
* 非递归,层序遍历
*/
public int depth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
int depth = 0;
queue.offer(root);
while (!queue.isEmpty()) {
int layerSize = queue.size();
for (int i = 0; i < layerSize; i++) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if ((node.right) != null) {
queue.offer(node.right);
}
}
depth++;
}
return depth;
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(3);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(4);
TreeNode node4 = new TreeNode(1);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
TreeOperation.show(roo1);
System.out.println(new TreeDepth().getDepth(roo1));
System.out.println(new TreeDepth().depth(roo1));
}
}
# 题目二 平衡二叉树
输入一棵二叉树,判断该二叉树是否是平衡二叉树。
本题应该是假定输入的已经是二叉搜索树,因为平衡二叉树首先是一颗二叉搜索树。平衡二叉树的定义是:对于任意结点,其左右子树的深度相差不超过1。
package com.lovedata.interview.N55_02_BalancedBinaryTree;
import utils.TreeNode;
import utils.TreeOperation;
/**
* @author pengshuangbao
* @date 2021/3/5 10:45 AM
*/
public class BalancedBinaryTree {
/**
* 方法1:递归地求每个结点的左右子树深度差,有重复计算
*/
public boolean isBalanceTree(TreeNode root) {
if (root == null) {
return true;
}
int left = getDepth(root.left);
int right = getDepth(root.right);
if (Math.abs(left - right) > 1) {
return false;
}
return isBalanceTree(root.left) && isBalanceTree(root.right);
}
public int getDepth(TreeNode root) {
if (root == null) {
return 0;
}
int left = getDepth(root.left);
int right = getDepth(root.right);
return left > right ? left + 1 : right + 1;
}
/**
* 方法2:后序遍历,为了传引用使用了对象数组
*/
public boolean isBalanceTree2(TreeNode root) {
if (root == null) {
return true;
}
//int类型不能传递,使用引用类型数组
int[] depth = new int[1];
return isBalanceTreeAfter(root, depth);
}
private boolean isBalanceTreeAfter(TreeNode root, int[] depth) {
if (root == null) {
depth[0] = 0;
return true;
}
//后续遍历,先遍历左边的;
boolean left = isBalanceTreeAfter(root.left, depth);
int leftDepth = depth[0];
//然后遍历右边的
boolean right = isBalanceTreeAfter(root.right, depth);
int rightDepth = depth[0];
//最后在判断中间的;
//当前节点的深度等于左边或者右边最大的加1
depth[0] = Math.max(leftDepth, rightDepth) + 1;
if (left && right && Math.abs(leftDepth - rightDepth) <= 1) {
return true;
}
return false;
}
public static void main(String[] args) {
TreeNode roo1 = new TreeNode(3);
TreeNode node1 = new TreeNode(2);
TreeNode node2 = new TreeNode(4);
TreeNode node4 = new TreeNode(1);
roo1.left = node1;
roo1.right = node2;
node1.left = node4;
TreeOperation.show(roo1);
System.out.println(new BalancedBinaryTree().isBalanceTree(roo1));
System.out.println(new BalancedBinaryTree().isBalanceTree2(roo1));
TreeNode node5 = new TreeNode(5);
node4.left = node5;
TreeOperation.show(roo1);
System.out.println(new BalancedBinaryTree().isBalanceTree(roo1));
System.out.println(new BalancedBinaryTree().isBalanceTree2(roo1));
}
}
# 面试题57--和为s的数字
# 题目1
输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S;如果有多对数字的和等于S,输出两个数的乘积最小的。
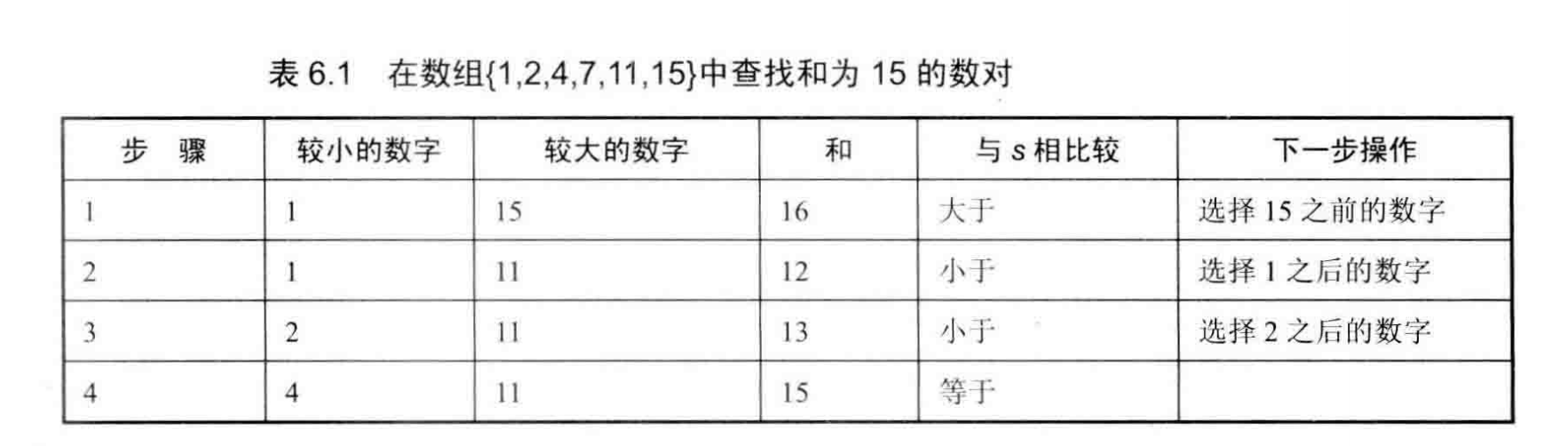
设置两个指针,一个指向数组的第一个元素,另一个指向数组的最后一个元素。即一开始将较小值设为数组的最小值,较大值设置为数组的最大值。
接下来求按照上面的方法不断与s比较,找到第一组和为s的两个数就是乘积最小的。
举个例子{1, 2, 4, 7, 11, 15}和数字15,刚开始1+15大于15,所以丢弃15;将1和11求和,小于15,所以丢弃1;将2和11求和,小于15,丢弃2;将4和11求和,刚好等于15,找到第一组和为15的两个数是4和11,它们乘积就是最小的。
package com.lovedata.interview.N57_01_TwoNumbersWithSum;
import java.util.ArrayList;
/**
* @author pengshuangbao
* @date 2021/3/8 3:47 PM
* 输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S;如果有多对数字的和等于S,输出两个数的乘积最小的。
*/
public class TwoNumbersWithSum {
public ArrayList<Integer> FindNumbersWithSum(int[] array, int sum) {
ArrayList<Integer> result = new ArrayList<Integer>();
if (array == null || array.length == 0) {
return result;
}
int low = 0;
int high = array.length - 1;
while (low < high) {
if (array[low] + array[high] == sum) {
result.add(array[low]);
result.add(array[high]);
break;
} else if (array[low] + array[high] < sum) {
low++;
} else {
high--;
}
}
return result;
}
public static void main(String[] args) {
int[] array = {1, 2, 4, 7, 11, 15};
System.out.println(new TwoNumbersWithSum().FindNumbersWithSum(array, 15));
}
}
# 面试题58--反转字符串
# 题目1
输入一个英文句子,翻转句子中单词的顺序,但单词内的顺序不变。为简单起见,标点符号和普通字母一样处理。 例如输入"I am a student."则输出"student. a am I"
比如字符串"I am a student.",整个翻转后得到".tneduts a ma I",然后翻转每个单词即可,将单词分隔开的依然是空格。该字符串有4个单词,做四次局部反转后就得到了结果"student. a am I"。
关键是要如何反转字符串的局部。可以设置两个指针,一个low指向局部字符串的头部,一个high指向局部字符串的尾部,一开始low和high都位于字符串的头部。当low指向的不是空格且high指向的字符是空格,此时就可以开始反转[low,high]内的字符串了....然后low和high继续向右移动,直到四个单词都被翻转。
package com.lovedata.interview.N58_01_ReverseWordsInSentence;
/**
* @author pengshuangbao
* @date 2021/3/9 11:07 AM
*
* 输入一个英文句子,翻转句子中单词的顺序,但单词内的顺序不变。为简单起见,标点符号和普通字母一样处理。
* 例如输入"I am a student."则输出"student. a am I"
*/
public class ReverseWordsInSentence {
public String reverseWords(String str) {
if (str == null || str.length() == 0) {
return null;
}
char[] chars = str.toCharArray();
int len = chars.length;
// 先整体反转 I am a student.",整个翻转后得到".tneduts a ma I"
reverse(chars, 0, len - 1);
// 两个指针,都是指向头部
int low = 0;
int high = 0;
// low 必须小于长度
while (low < len) {
if (chars[low] == ' ') {
//如果low是空格,则low和high都得往后移动
++low;
++high;
} else if (high == len || chars[high] == ' ') {
// 否则,如果 high = len 并且 high 是空格的时候,则是一个单词,就得单独反转这个单词
// 因为high是空格,所以要 --high
reverse(chars, low, --high);
// 然后,将low置于当前high的下一个位置
low = ++high;
} else {
// low 和 high 都不是空格,则high往后加
high++;
}
}
return new String(chars);
}
public void reverse(char[] chars, int low, int high) {
while (low < high) {
char c = chars[low];
chars[low] = chars[high];
chars[high] = c;
low++;
high--;
}
}
public static void main(String[] args) {
String s = "hello";
char[] chars = s.toCharArray();
new ReverseWordsInSentence().reverse(chars, 0, s.length() - 1);
System.out.println(chars);
String s1 = "I am a student.";
System.out.println(new ReverseWordsInSentence().reverseWords(s1));
}
}
# 题目2
字符串的左旋操作是把字符串前面的若干个字符转移到字符串的尾部。 比如输入字符串"abcdefg"和一个数字2,则左旋转后得到字符串"cdefgab"
# 方法2:三次翻转——先局部翻转再整体翻转
举个简单的例子"hello world",按照上题的要求,会得到"world hello". 而在此题中,假如要求将前五个字符左旋转,会得到" worldhello"(注意w前哟一个空格),是不是接近了。
所以本题可以延续上题的思路,不过这次先局部翻转再整体反转。如字符串"abcdefg"要求左旋转前两个字符,先反转ab和cdefg得到bagfedc,然后反转这个字符串得到cdefgab即是正确答案。
package com.lovedata.interview.N58_02_LeftRotateString;
/**
* @author pengshuangbao
* @date 2021/3/9 11:45 AM
* 字符串的左旋操作是把字符串前面的若干个字符转移到字符串的尾部。
* 比如输入字符串"abcdefg"和一个数字2,则左旋转后得到字符串"cdefgab"
*/
public class LeftRotateString {
public String leftRotateString2(String str, int n) {
if (str == null || str.length() == 0) {
return null;
}
char[] chars = str.toCharArray();
reverse(chars, 0, n - 1);
reverse(chars, n, str.length() - 1);
reverse(chars, 0, str.length() - 1);
return new String(chars);
}
public void reverse(char[] chars, int low, int high) {
while (low < high) {
char c = chars[low];
chars[low] = chars[high];
chars[high] = c;
low++;
high--;
}
}
public static void main(String[] args) {
String a = "abcdefg";
System.out.println(new LeftRotateString().leftRotateString2(a, 2));
}
}
# 面试题59--队列的最大值
# 滑动窗口的最大值
题目1:滑动窗口的最大值。 给定一个数组和滑动窗口的大小,请找出所有滑动窗口里的最大值。例如,如果输入数组{2, 3, 4, 2, 6, 2, 5}以及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}
# 方法1:基于最大堆的优先队列
就以题目中的例子来模拟找出窗口中的最大值的过程。先存入3个元素,于是优先队列中有{2, 3, 4},使用peek方法可以以O(1)的时间得到最大值,之后删除队列头的元素2,同时入列下一个元素,此时队列中有{3, 4, 2},再调用peek方法得到最大值,然后删除队列头的3,下一个元素入列......不断重复进行此操作,直到最后队列中只有两个元素为止。
package com.lovedata.interview.N59_01_MaxInSlidingWindow;
import java.util.*;
/**
* @author pengshuangbao
* @date 2021/3/9 2:39 PM
* 题目1:滑动窗口的最大值。
* 给定一个数组和滑动窗口的大小,请找出所有滑动窗口里的最大值。例如,如果输入数组{2, 3, 4, 2, 6, 2, 5}以及滑动窗口的大小3,
* 那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}
*/
public class MaxInSlidingWindow {
/**
* 方法1:使用优先队列
*/
public ArrayList<Integer> maxInWindows(int[] num, int size) {
ArrayList<Integer> list = new ArrayList<>();
if (num == null || num.length < size || size <= 0) {
return list;
}
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
int j = 0;
for (int i = 0; i < num.length; i++) {
maxHeap.offer(num[i]);
if (maxHeap.size() >= size) {
list.add(maxHeap.peek());
maxHeap.remove(num[j++]);
}
}
return list;
}
}
# 队列的最大值
定义一个队列,实现max方法得到队列中的最大值。要求入列、出列以及邱最大值的方法时间复杂度都是O(1)
此题和面试题30“包含min的栈”同一个思路。
一个dataQueue正常入列、出列元素,为了以O(1)的时间获取当前队列的最大值,需要使用一个maxQueue存放当前队列中最大值。具体来说就是,如果即将要存入的元素比当前最大值还大,那么存入这个元素;否则再次存入当前最大值。
package com.lovedata.interview.N59_02_QueueWithMax;
import java.util.Deque;
import java.util.LinkedList;
import java.util.Queue;
/**
* @author pengshuangbao
* @date 2021/3/9 2:50 PM
* 定义一个队列,实现max方法得到队列中的最大值。要求入列、出列以及邱最大值的方法时间复杂度都是O(1)
*/
public class QueueWithMax {
private Deque<Integer> dataQueue = new LinkedList<>();
private Deque<Integer> maxQueue = new LinkedList<>();
public void offer(int number) {
dataQueue.offer(number);
// 如果 maxQueue 是空,证明还没数据进来,或者 maxQueue的最大值小于当前的值,则放入到队列投
if (maxQueue.isEmpty() || number > maxQueue.peek()) {
maxQueue.offerFirst(number);
} else {
maxQueue.offerFirst(maxQueue.peekFirst());
}
}
public void poll() {
if (dataQueue.isEmpty()) {
throw new RuntimeException("队列位空");
}
dataQueue.poll();
maxQueue.poll();
}
public int max() {
if (maxQueue.isEmpty()) {
throw new RuntimeException("队列已空");
}
return maxQueue.peekFirst();
}
}
还是上面的例子{2, 3, 4, 2, 6, 2, 5},分析随着各个元素入列dataQueue和maxQueue的情况。
| 操作 | dataQueue | maxQueue | max |
|---|---|---|---|
| 2入列 | 2 | 2 | 2 |
| 3入列 | 2, 3 | 3, 2 | 3 |
| 4入列 | 2, 3, 4 | 4, 3, 2 | 4 |
| 2入列 | 2, 3, 4, 2 | 4, 4, 3, 2 | 4 |
| 6入列 | 2, 3, 4, 2, 6 | 6, 4, 4, 3, 2 | 6 |
| 2入列 | 2, 3, 4, 2, 6, 2 | 6, 6, 4, 4, 3, 2 | 6 |
| 5入列 | 2, 3, 4, 2, 6, 2, 5 | 6, 6, 6, 4, 4, 3, 2 | 6 |
出列的话两个队列同时出列一个元素,保证了maxQueue的队列头元素始终是dataQueue的当前最大值。